Gli smartphone hanno al loro interno un accelerometro (in realtà sono tre, uno per ciascun asse) per determinare come muoviamo il nostro dispositivo e per consentirci di pilotare aerei, astronavi e pupazzetti vari. Vi sono app gratuite (vedi la nota in calce per una lista) che permettono di visualizzare e graficare l’accelerazione misurata e salvare i dati su file di testo. Con questi programmi è possibile studiare molti dei fenomeni propri della meccanica classica e riscoprire il principio alla base della teoria della relatività generale.
Gli accelerometri fanno parte della famiglia dei MEMS, Sistemi Micro-Elettro-Meccanici (Micro ElectroMechanical Systems). Queste micromacchine sono composte da meccanismi in silicio e hanno dimensioni che raramente superano la frazione di millimetro. Questi microscopici ingranaggi, leve e bilance sono opportunamente sagomati e realizzati con tecniche litografiche analoghe a quelle con cui si realizzano i processori dei computer.
Questi accelerometri sono costituiti da una massa centrale, libera di muoversi e collegata con delle microscopiche molle alla struttura esterna, fissa e solidale con lo smartphone. Quando agitiamo il telefono, la massa centrale rimane ferma, essendo sconnessa dal resto del telefono. Caricando elettricamente questi due elementi, abbiamo a disposizione un microscopico condensatore la cui capacità – e dunque il cui segnale elettrico – varia a seconda delle oscillazioni e viene captato e utilizzato dal processore dello smartphone.
Appoggiando il cellulare sul tavolo possiamo misurare l’accelerazione di gravità: essa risulta diretta verso il basso lungo l’asse ortogonale allo schermo ed è pari a 9.8 m/s2 (1g). Possiamo farci un’idea della sensibilità dello strumento facendo vibrare il tavolo o lasciando cadere piccoli oggetti sul tavolo (qual è il più piccolo che viene rivelato? Riuscite a misurare una penna? Un fagiolo? E un granello di sale?): a seconda dell’intensità delle scosse vedremo apparire accelerazioni dell’ordine di un centesimo o un decimo di g (si possono anche superare i 2 g ma attenzione a non rompere il cellulare!).
Ponendo il telefono sul pavimento di un ascensore possiamo misurare come la forza di gravità sembri aumentare quando la cabina inizia a salire e sembri diminuire quando essa rallenta per fermarsi. In entrambi i casi, sia noi sia il cellulare risentiamo di una forza aggiuntiva, o apparente, dovuta alla prima legge di Newton, conseguenza del fatto che tendiamo a permanere nel nostro stato di quiete (alla partenza, dove questa forza si somma a g) o di moto (all’arrivo, quando essa si sottrae a g). Le accelerazioni misurate sono molto piccole (circa il 5% di g) ma percepibili e misurabili.
Ponendo il telefono su un’altalena e facendolo ondeggiare potremo poi osservare le oscillazioni del vettore di gravità e misurare l’aggiuntiva forza centrifuga (possiamo anche legarlo a un filo e farlo dondolare, ma in quel caso bisogna fare attenzione alle vibrazioni aggiuntive indotte dal filo e dalla nostra mano).
Una serie di dati ancora più interessanti si ottengono poggiando il telefono su un veicolo in movimento, osservando e confrontando i diversi comportamenti che si tipici delle automobili dei treni, degli aerei o delle navi.
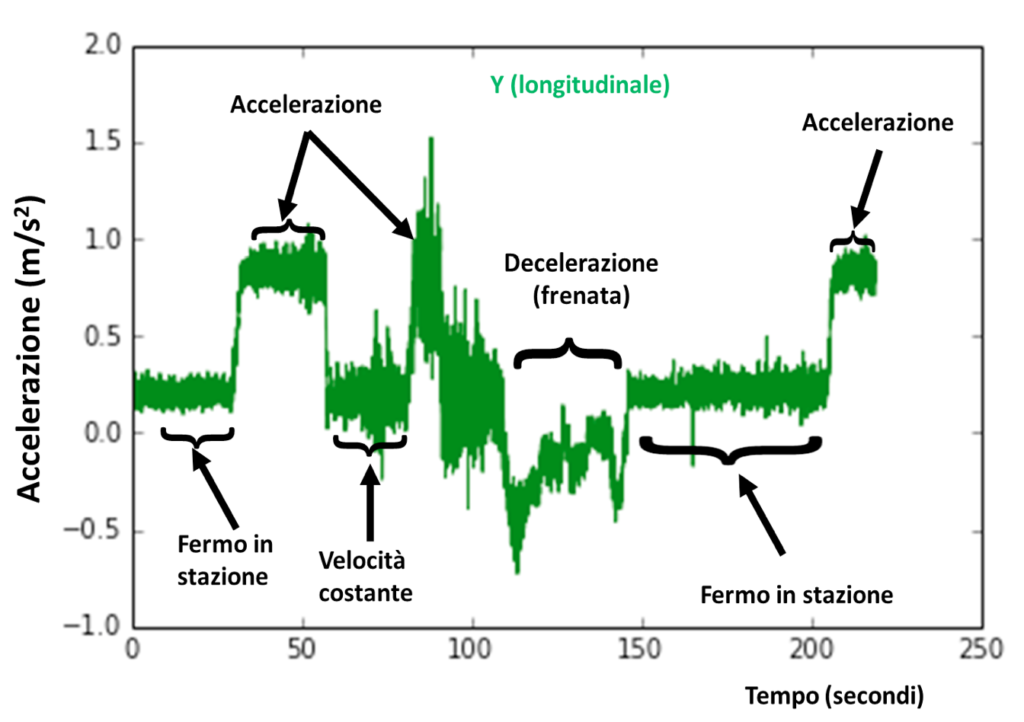
Nel caso del treno l’asse più interessante è quello diretto nella direzione di marcia delle carrozze. In figura possiamo vedere l’accelerazione cui siamo soggetti quando parte e le frenate (accelerazione negativa) quando si ferma in stazione.
Tuttavia, l’esperimento più semplice e al tempo stesso più cruciale punta al cuore di uno di dei più grandi misteri della fisica moderna: per effettuarlo basta lasciare cadere il telefono a terra (possibilmente su un cuscino). Mentre lo smartphone è in caduta libera, la sua accelerazione è pari a g e dunque nel suo sistema di riferimento uniformemente accelerato non risente della forza di gravità, che sembra annullarsi.
Questo effetto è lo stesso percepito dagli astronauti in orbita intorno alla Terra (in quel caso è la forza centrifuga ad annullare gli effetti di quella gravitazionale) e dai passeggeri dei voli suborbitali come quelli di Blue Origin e Virgin Galactic e dei voli parabolici degli aerei a zero-g (detto Vomit Comet, per gli indesiderati effetti collaterali che induce nello stomaco dei passeggeri).
Questo fenomeno è dovuto al fatto che la massa inerziale (quella dell’accelerazione) e quella gravitazionale sono (per qualche sconosciuto motivo) le stesse:
minerziale = mgravitazionale
per cui se scriviamo la legge di Newton:
minerziale a = mgravitazionale g
abbiamo
a=g
indipendentemente dalla massa dei corpi coinvolti, che infatti cadono alla stessa maniera, come fu osservato da Galileo alla fine del 1500.
Tuttavia, nessuno conosce il motivo di questa fondamentale uguaglianza. Si tratta di una proprietà unica del campo gravitazionale, non riscontrata nelle altre tre forze fondamentali della natura.
Il Principio di equivalenza tra massa inerziale e quella gravitazionale e è alla base della teoria della Relatività Generale. Einstein partì proprio da questo postulato basandosi sulle osservazioni sperimentali. Anche se la relatività generale è una delle teorie con le più precise conferme sperimentali, la teoria che si cela dietro il principio di equivalenza ci elude completamente e probabilmente continuerà a farlo nei secoli a venire
FARE SCIENZA
Studiamo la meccanica con lo smartphone fuori classe
Portate lo smartphone su una macchina radiocomandata, su una barca, su una bicicletta, in aereo. Alcune delle app riportate sotto possono effettuare anche la trasformata di Fourier delle accelerazioni, mostrando così le frequenze di vibrazione principali dei vari mezzi.
Note:
1. App suggerite:
https://play.google.com/store/apps/details?id=de.rwth_aachen.phyphox
https://apps.apple.com/us/app/phyphox/id1127319693
https://play.google.com/store/apps/details?id=com.chrystianvieyra.physicstoolboxsuite
https://apps.apple.com/jp/app/physics-toolbox-sensor-suite/id1128914250
https://play.google.com/store/apps/details?id=pt.acoelhosantos.android.acc
2. Il segnale degli accelerometri MEMS presenta di solito una banda per via delle fluttuazioni delle letture dell’accelerometro. Queste fluttuazioni ci forniscono anche l’errore associato alla misura (circa 0.05 m/s2) e mostrano come i MEMS siano strumenti intrinsecamente ‘rumorosi’ che richiedono del processamento matematico per essere usati come strumenti di misura.
3. L’area sotto la curva in figura rappresenta l’integrale dell’accelerazione ossia la velocità del treno a un dato istante. Se l’accelerazione è negativa e il treno sta frenando allora la velocità sta diminuendo. Alle stazioni sappiamo che il treno è fermo, per cui l’area complessiva (tenendo conto del segno) deve essere pari a zero. La distanza percorsa è pari all’integrale della velocità.
