
In natura, si possono trovare innumerevoli esempi di formazione di pattern, cioè di conformazioni spaziali che presentano una certa regolarità o simmetria. Il caso più immediato a cui siamo portati a pensare è senza dubbio la pigmentazione degli animali. Dalle strisce delle zebre alle macchie dei leopardi, passando per disegni molto più complicati sulle ali delle farfalle, l’evoluzione ha dato sfoggio di tutta la sua creatività. In realtà, si possono trovare pattern anche in altri contesti, come nei paesaggi soggetti a desertificazione, in alcuni particolari fenomeni atmosferici o nelle reazioni chimiche. La domanda di chi studia modelli matematici è: siamo in grado di capire e descrivere i meccanismi microscopici che portano alla formazione di pattern?

Il modello di Turing
La stessa domanda era già stata formulata da un matematico famoso per il suo contributo in ben altre aree della matematica: Alan Turing. In un suo articolo del 1952 “The Chemical Basis of Morphogenesis“, infatti, propose un modello matematico che potesse spiegare la morfogenesi, letteralmente la creazione delle forme, sul manto degli animali.
Il modello si basa sul meccanismo di reazione-diffusione. Vengono prese in considerazione due quantità (di molecole, di cellule o di organismi) detti, appunto, “morfogeni”, che hanno la possibilità di diffondersi su una certa area spaziale e allo stesso tempo di interagire tra loro. In questa dinamica, il ruolo della diffusione è fondamentale. Bisogna, infatti partire da una condizione di equilibrio spazialmente omogeneo, cioè mettersi nelle condizioni in cui, senza la diffusione, i due morfogeni sarebbero distribuiti in modo uniforme su tutto lo spazio. Ma quando si tiene conto della diffusione, questo equilibrio si rompe (da qui l’espressione “instabilità di Turing”, usata per descrivere questo fenomeno) e le due quantità si aggregano in modo eterogeneo nello spazio, creando strisce, macchie o strutture a labirinto.
Un particolare modo in cui i due morfogeni possono interagire è chiamato di tipo attivatore-inibitore. La quantità che ha il ruolo di attivatore è sia in grado di autoriprodursi che di stimolare la produzione della quantità che fa da inibitore. D’altra parte, l’inibitore andrà a ostacolare la formazione dell’attivatore. In questo caso, per la formazione dei pattern, è fondamentale che la velocità con cui si diffonde l’inibitore sia maggiore quella dell’attivatore.
L’applicazione di queste teorie alla formazione delle fantasie presenti nel regno animale si basa sulla diffusione (sulla pelle dell’embrione) delle cellule responsabili della pigmentazione e di un attivatore chimico, che ne stimolerà o meno l’attivazione di determinati geni.
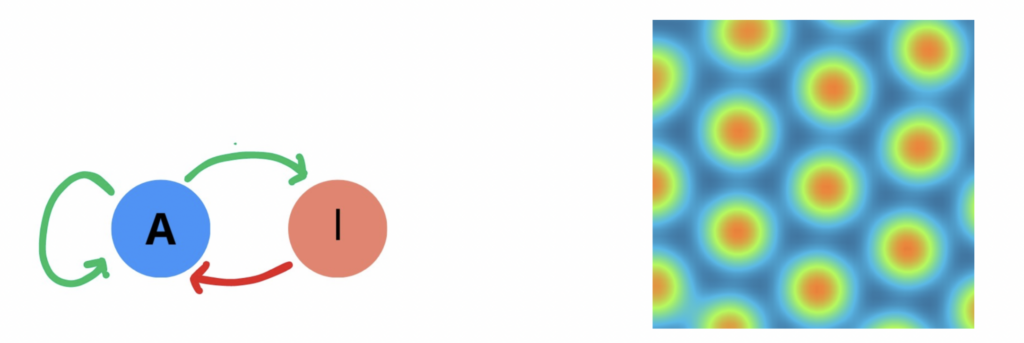
A destra: Concentrazione delle cellule che reagiscono con l’attivatore ottenuta simulando tramite computer il modello di Turing
In realtà, dai primi studi che sono stati fatti negli anni Ottanta e Novanta, ci sono stati molti sviluppi. In particolare si è visto che ci sono diversi altri meccanismi cellulari, più complessi, che possono dare origine alla formazione di pattern. Nel caso del pesce zebra, è stato osservato che il meccanismo non è quello della diffusione di cellule regolate da un’altra sostanza. Ci sono invece due popolazioni di cellule, i melanofori responsabili della colorazione nera e gli xantofori responsabili della colorazione gialla, che si stimolano o sopprimono a vicenda, interagendo attraverso delle protuberanze. Nonostante ciò il modello di Turing si presta comunque in maniera efficiente alla riproduzione dei pattern tramite software.
Macchie e strisce
Uno studio completo e approfondito di come si possa riprodurre la formazione di pattern in natura attraverso i modelli è stato prodotto da James Murray negli anni Ottanta. In particolare è riuscito, basandosi sulla teoria di Turing, a spiegare in modo dettagliato come sulla pelliccia dei mammiferi possano formarsi macchie o strisce.
Un concetto fondamentale a questo proposito è quello dei “modi instabili”. Studiando l’instabilità di Turing con gli strumenti matematici, infatti, l’obiettivo è descrivere la concentrazione dei morfogeni come funzioni dipendenti da tempo e spazio. Per farlo, queste funzioni si esprimono come somme di termini, alcuni dei quali hanno delle determinate caratteristiche che li rendono l’origine dell’instabilità. Questi termini vengono detti, appunto, modi instabili. Di solito c’è un modo instabile dominante, indicato con un intero k, che ci dà informazioni sul numero di strisce o macchie che si andranno a formare sulla pelliccia dell’animale. Supponendo di poter approssimare la pelle dell’embrione, su cui si diffondono i morfogeni, come un rettangolo di larghezza l e altezza h, abbiamo la relazione
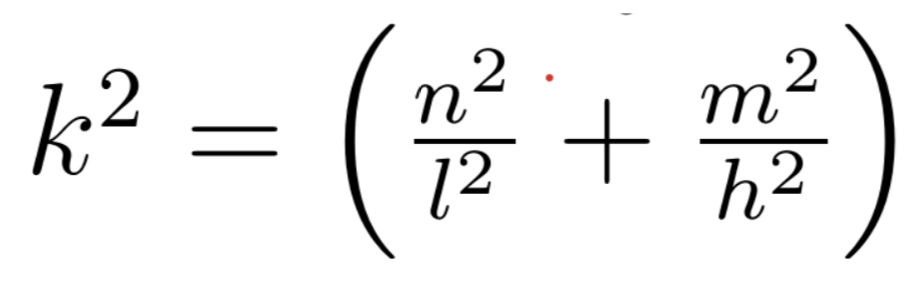
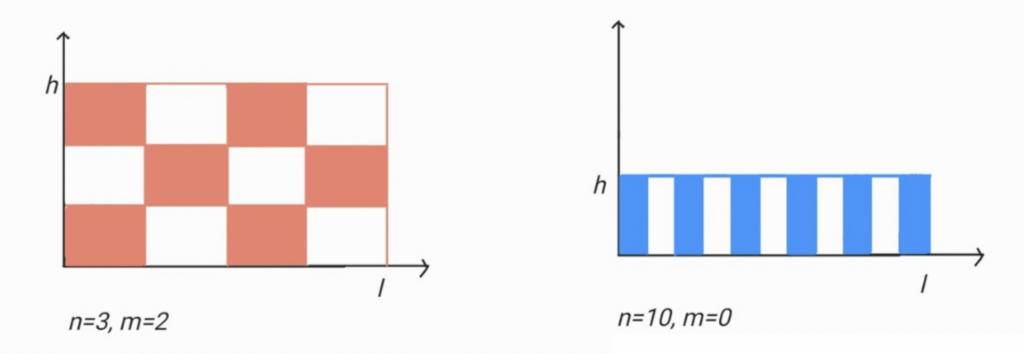
I due interi n e m rappresentano il numero di “passaggi” da un colore all’altro lungo la direzione rispettivamente orizzontale e verticale.
Un esempio pratico sta nella spiegazione del perché il leopardo presenta macchie su tutto il corpo ma la coda è a strisce orizzontali. Il corpo, infatti, può essere approssimato a un “quadrato”, cioè l e h hanno dimensioni simili e possiamo trovare diversi valori per n e m. Questo si traduce nella comparsa delle macchie. Sulla coda, invece, che può essere vista come un rettangolo stretto e lungo, l è decisamente maggiore di h. Il risultato è che non avremo nessun valore per m e molti valori per n, da cui la comparsa delle strisce.
Il risultato pioneristico di Turing continua ad essere oggi il punto di partenza fondamentale per studi che vanno ben oltre la formazione di pattern per gli esempi citati. Numerose applicazioni, infatti, riguardano le scienze sociali per lo studio di aggregazione di individui, la creazione di nuclei di criminalità o di focolai infettivi; oppure lo studio di condizioni mediche che portano alla formazione di placche e lesioni, come la sclerosi multipla. In ogni caso, questi modelli permettono di vedere come l’interazione tra entità singole porti a caratteristici fenomeni a più ampia scala di osservazione.
Proposte di attività didattiche:
Far compiere ai ragazzi una ricerca sulla formazione di pattern in natura, con particolare attenzione agli animali.
Una volta raccolte alcune immagini di esempi di macchie o strisce, fargli stimare le dimensioni dell’area spaziale (l e h) nella formula, fargli contare i passaggi da un colore all’altro (m ed n) e fargli così calcolare il k del corrispondente modo instabile.
