
La distribuzione Normale è un oggetto matematico di importanza centrale in campi come la probabilità e la statistica. Per capirlo partiamo da un semplice esperimento: ci basterà essere un gruppo di persone abbastanza numeroso. Prendiamo, per esempio, una classe di 30 alunni. Chiediamo a ognuno di loro di lanciare una moneta cinque volte e di assegnare il punteggio 1 se esce testa e 0 se esce croce, sommando a ogni lancio. Il punteggio, quindi, varierà da 0 a 5. Poi costruiamo un grafico a barre riportando il punteggio sull’asse delle ascisse e quanti alunni hanno riportato quel punteggio sull’asse delle ordinate. A questo punto ripetiamo la stessa operazione ma aumentando il numero di lanci a testa. Si potrà osservare che il grafico ottenuto somiglierà sempre di più a quello riportato nella Figura 1. In particolare, il valore più alto nel grafico corrisponderà alla metà del numero di lanci.
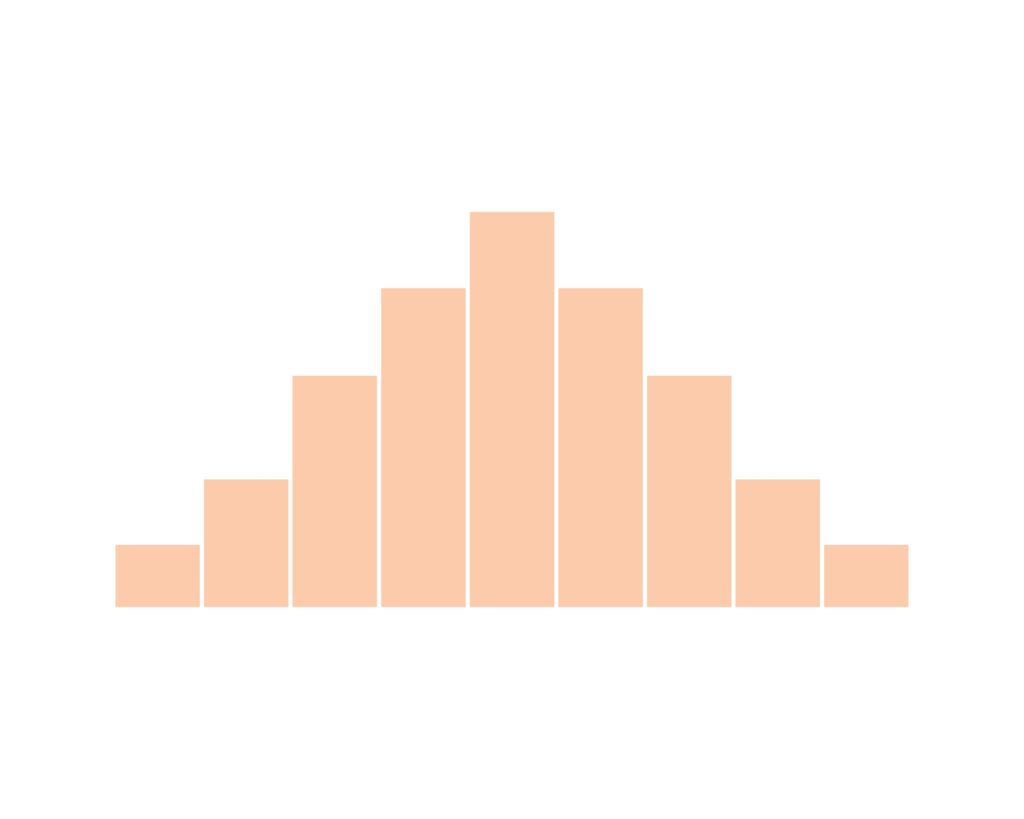
In termini probabilistici, questa analisi può essere usata per rispondere alla seguente domanda: “qual è la probabilità che si ottenga testa poche volte?”. La probabilità ovviamente sarà molto bassa, invece la probabilità che si ottenga metà delle volte testa e metà delle volte croce è molto alta. Questo fenomeno è sempre stato molto conosciuto: già nel Fedone di Platone, libro risalente al IV secolo a.C, si legge:
«Non ti sei mai accorto che in tutte le cose gli estremi sono rari mentre gli aspetti intermedi sono frequenti, anzi numerosi?».
A questo punto, però, vogliamo dare una lettura del nostro esperimento in chiave matematica, ossia vogliamo una legge che ci permetta di associare a ogni valore l’esatta probabilità di ottenerlo. A questo risultato arrivò per primo il matematico francese Abraham de Moivre nel 1733, durante i suoi studi sulla probabilità. De Moivre intuì che, all’aumentare del numero di prove, il grafico si avvicinava sempre di più a una particolare curva, come riportato nella Figura 2, che per la sua forma prende il nome di “curva a campana”.
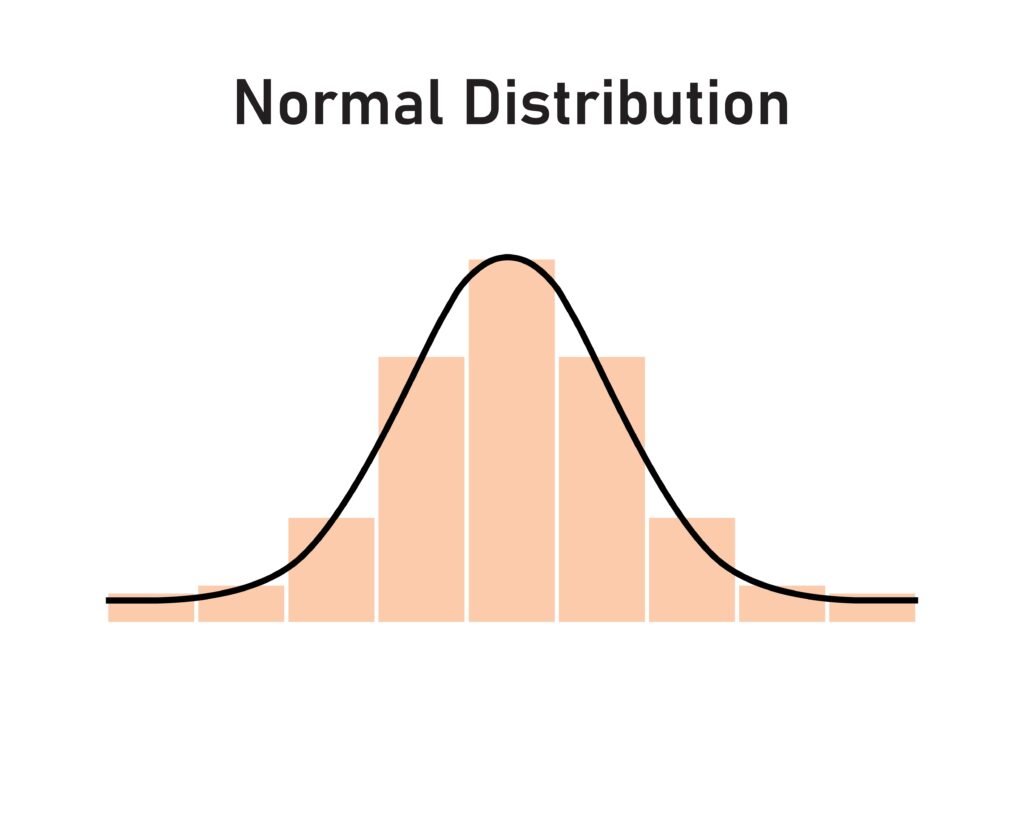
Tale curva, è il grafico di una particolare funzione, detta distribuzione Gaussiana, essendo stata ampiamente usata dal matematico Carl Friedrich Gauss agli inizi dell’Ottocento, e che più avanti nello stesso secolo cominciò ad essere chiamata “Normale”. La funzione in questione ha la seguente espressione:
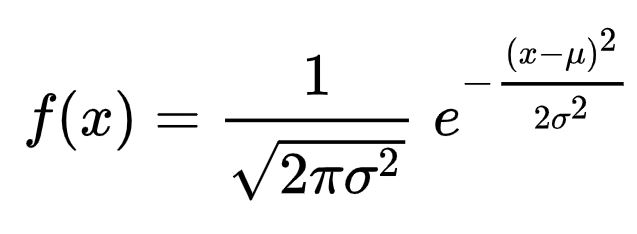
dove μ è la media, cioè il valore in corrispondenza del quale si ha il picco della campana, mentre σ^2 è la varianza, ossia una misura di quanto i dati raccolti si discostano dalla media. L’intuizione di de Moivre diventerà poi un risultato centrale della teoria probabilistica, noto come “Teorema di limite centrale”, che fornisce una dimostrazione rigorosa del fatto che, se il numero di prove effettuate tende all’infinito, la distribuzione delle probabilità sarà esattamente quella data dalla Normale.
La distribuzione normale è stata usata in ogni ambito scientifico che richiedesse la raccolta di misurazioni da cui estrapolare una legge generale per un dato fenomeno. Tra i maggiori contributi in questo senso se ne possono citare due.
Uno è quello dello scienziato britannico Francis Galton (1822–1911), attivo nei campi della statistica, della psicologia sperimentale, dell’antropologia e della geografia. Data la sua parentela con Charles Darwin, lavorò su svariati aspetti dell’eredità biologica e delle differenze individuali. È anche noto per aver inventato la Macchina di Galton, un dispositivo che permette di osservare praticamente il principio alla base del Teorema del limite centrale.
Il secondo è quello dato dai due fisici James Clerk Maxwell (1831 – 1879) e Ludwig Eduard Boltzmann (1844 – 1906). In particolare, gli studi del secondo sulla termodinamica hanno permesso di ricavare un risultato tuttora fondamentale per il comportamento di gas rarefatti. Infatti, considerando un insieme di molecole dello stesso gas aventi massa m e supponendo che il gas sia all’equilibrio, ad una certa temperatura T, la legge che ci dice come è distribuita la velocità v delle molecole di gas è
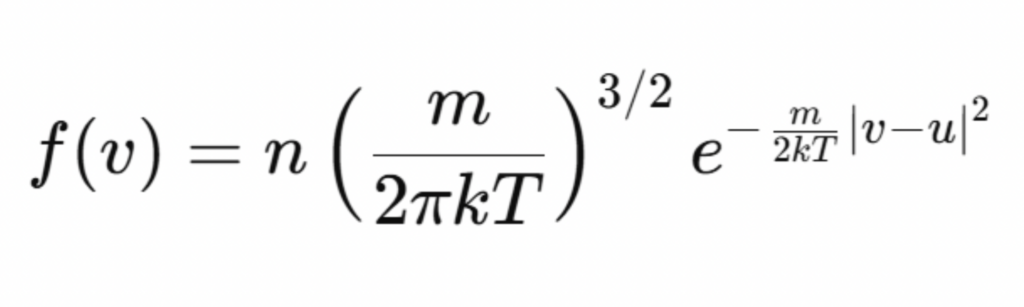
dove n è la densità del gas, u la velocità media delle molecole e k è la costante di Boltzmann. Questa particolare distribuzione Gaussiana era stata introdotta da Maxwell e, pertanto, viene indicata come distribuzione Maxwelliana.
L’importanza della distribuzione Normale risiede nel fatto che per un gran numero di esperimenti, dalla biologia alla fisica, come si è detto, basta un numero abbastanza grande di prove per poter supporre che il dato che stiamo misurando segua questa legge. Tornando all’esempio iniziale, supponiamo di avere abbastanza tempo e pazienza da effettuare mille lanci: possiamo allora tranquillamente sostenere che la distribuzione delle misure effettuate possa essere rappresentata con una curva a campana, con la distribuzione che avrà una certa media μ (pari a 500) e una certa varianza σ^2 (che la probabilità ci dice essere 250).
Infine, la Gaussiana trova larga applicazione nei metodi della statistica inferenziale. Questa disciplina si occupa, di ricavare informazioni su un’intera popolazione (ad esempio l’altezza media) partendo dai dati raccolti su un singolo campione. Naturalmente i valori ottenuti tramite un’analisi inferenziale non corrispondono esattamente a quelli reali, ma possiamo sapere qual è il margine di errore che stiamo commettendo, che sarà tanto più piccolo quanto è più grande il campione scelto.
Attività didattica:
Dopo la visione del video sulla macchina di Galton, gli alunni vengono disposti in fila indiana e a ciascuno viene consegnata una moneta. Il primo alunno compie un passo avanti e lancia la moneta: in base al risultato (testa o croce) si sposta rispettivamente verso destra o verso sinistra. Il procedimento continua con ulteriori lanci, fino al raggiungimento della parete opposta dell’aula. L’attività viene ripetuta per ogni alunno. Al termine dell’esperimento, si osserva come la maggior parte degli studenti si trovi concentrata nella zona centrale della parete, mentre solo pochi si distribuiscono verso i bordi. Il risultato simula visivamente il comportamento della distribuzione normale.
