
In fatto di ecologia, siamo abituati a sentir parlare di questioni come specie a rischio di estinzione o di impatto di caccia e pesca sulle popolazioni di alcuni animali. Ma, oltre ad affermare che alcune specie stanno scomparendo, siamo in grado di dire con precisione in che modo, con quale velocità e in base a quali particolari fattori lo stanno facendo?
In questo caso, la matematica ci aiuta. Esiste, infatti, un’area della matematica, la biomatematica, che si occupa esattamente di questo: costruisce dei modelli che possano descrivere l’andamento di una popolazione di esseri viventi nel tempo e, quindi, prevedere in qualche modo anche la loro sorte futura.
Gli studi di Lotka e Volterra
Fu esattamente un secolo fa, durante gli anni Venti del Novecento, che due matematici, l’inglese Alfred Lotka e l’italiano Vito Volterra, cominciarono a sviluppare le teorie alla base della biomatematica. Anche se i loro lavori furono del tutto indipendenti l’uno dall’altro, ricavarono quasi in contemporanea il modello che oggi porta il nome di entrambi, partendo dalla stessa ambizione: applicare i principi che regolavano i processi fisici e chimici alla biologia e studiarli mediante strumenti matematici.
Alfred Lotka (1880-1949) fu uno studioso inglese trasferitosi negli Stati Uniti agli inizi del Novecento con l’intenzione di istituire una nuova disciplina, la “Biologia fisica”. La sua visione si basava sul fatto che, come nella chimica l’interazione tra molecole poteva essere descritta da leggi matematiche fondate sullo scambio di materia ed energia, allo stesso modo i sistemi biologici potevano essere visti come l’interazione tra organismi governata dallo scambio di cibo e risorse. Era, pertanto, scopo del suo studio formulare delle leggi che rappresentassero la dinamica di popolazioni (aumento o diminuzione di individui) in termini di interazioni tra specie, consumo delle risorse e riproduzione.
In questa cornice, il lavoro di Lotka del 1920, in cui veniva descritto l’andamento di una popolazione di erbivori in relazione con la pianta di cui si cibavano, presentava già il risultato fondamentale del modello, cioè una ciclicità nella crescita e decrescita delle due specie coinvolte. Tali risultati furono poi estesi alle dinamiche di sistemi composti da una popolazione di prede e una di predatori oppure da una di parassiti e una di organismi ospitanti.
Vito Volterra (1860-1940) è uno dei nomi più rilevanti nel panorama matematico degli inizi del XX secolo. Come Lotka, Volterra coltivava il progetto di applicare i principi rigorosi della meccanica razionale alle scienze naturali. Per questo motivo, prestò grande interesse alle statistiche condotte dal genero Umberto D’ancona, biologo marino, tra il 1905 e il 1923, sul pesce pescato nel mare Adriatico. In particolare, focalizzò l’attenzione sul rapporto tra la quantità di pesci predatori e di quelli preda, osservando che, durante gli anni della Seconda Guerra Mondiale, quando le attività di pesca si trovarono a essere notevolmente rallentate, venivano pescati, in percentuale, molti più pesci appartenenti alle specie di predatori.
La volontà di trovare un’equazione che descrivesse il modo in cui interagivano le popolazioni e che rispecchiasse i dati empirici portò Volterra a formulare il modello analogo a quello di Lotka.
Il modello di Volterra
Il modello parte proprio dal considerare il comportamento di due popolazioni di individui, una di prede e una di predatori, e osservare il loro andamento nel tempo. Matematicamente questo corrisponde a vedere le popolazioni come funzioni del tempo e a studiare le loro derivate. La variazione delle prede (P) nel tempo è data, da una parte, da quanto la popolazione crescerebbe in assenza di interazione con i predatori, che dipende dal tasso di natalità (b) e, d’altra parte, da quanto l’incontro tra predatori (N) e prede determina una diminuzione di quest’ultime, dato un fattore di impatto (c). In formule:
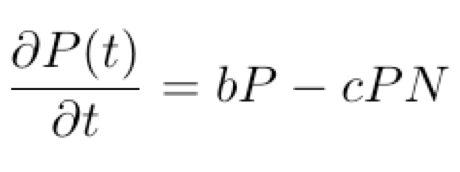
Il comportamento dei predatori (N), invece, è governato dal fatto che ci sarebbe un certo tasso di mortalità (d) che porterebbe alla decrescita della popolazione se non ci fossero prede e dall’aumento, invece, dovuto all’interazione con esse, anche stavolta regolato da un determinato fattore (e). L’equazione risultante è:
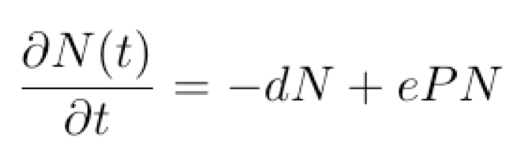
Ricavando poi, dallo studio delle due equazioni, il comportamento delle due popolazioni nel tempo, si trova una struttura ciclica. Se le prede aumentano, infatti, i predatori avranno più cibo e quindi aumenteranno a loro volta. Ma, se i predatori aumentano, cacceranno di più, quindi ci sarà una più elevata mortalità delle prede, che porterà a una diminuzione dei predatori a causa della scarsità di cibo. Questo permetterà alle prede di aumentare di nuovo, ricominciando il ciclo.

Ovviamente, un modello che prevede che la sopravvivenza o la morte di due popolazioni dipendano esclusivamente una dall’altra è decisamente semplicistico, ma quando fu introdotto permise comunque di fornire una solida base teorica ai dati sperimentali. Lo stesso sistema di equazioni ha trovato applicazione in diversi ambiti, come l’epidemiologia, la chimica delle combustioni o l’economia.
FARE SCIENZE
Simulare la dinamica delle due popolazioni in classe
Formare due piccoli gruppi di studenti che rappresentano le prede e i predatori. Far “nascere” le prede aggiungendo ragazzi al gruppo. Per ogni ragazzo che si aggiunge, far aggiungere (uno o più) ragazzi al gruppo dei predatori. Per ognuno che si è aggiunto ai predatori, togliere (una o più) prede e, di conseguenza, togliere anche predatori. Per ogni predatore andato via, aumentare di nuovo il numero delle prede. Far osservare ai ragazzi che, se per ogni predatore che si aggiunge, vengono sottratte molte prede (per simulare il fenomeno di caccia e pesca non controllate) si arriva all’estinzione di entrambe le popolazioni.
