Nel mio precedente articolo ho proposto una lezione di geometria tra le pieghe origami sul modello di una squadretta con angoli di 45° e 90°. Completiamo ora il kit da disegno piegando un semplice modello origami sempre creato da Paolo Bascetta (insegnante di Liceo scientifico ed esperto di origami) per ottenere una squadretta di 30°, 60° e 90°. Questa volta ci concentreremo sull’analisi degli angoli che si formano naturalmente nella costruzione. Come la scorsa volta, l’attività principale è pensata per ragazzi dagli 11 ai 15 anni, ma darò alcuni spunti anche per i più grandi.
Anche in questo caso per piegare il modello si parte da un foglio A4 (o da suoi multipli o sottomultipli).
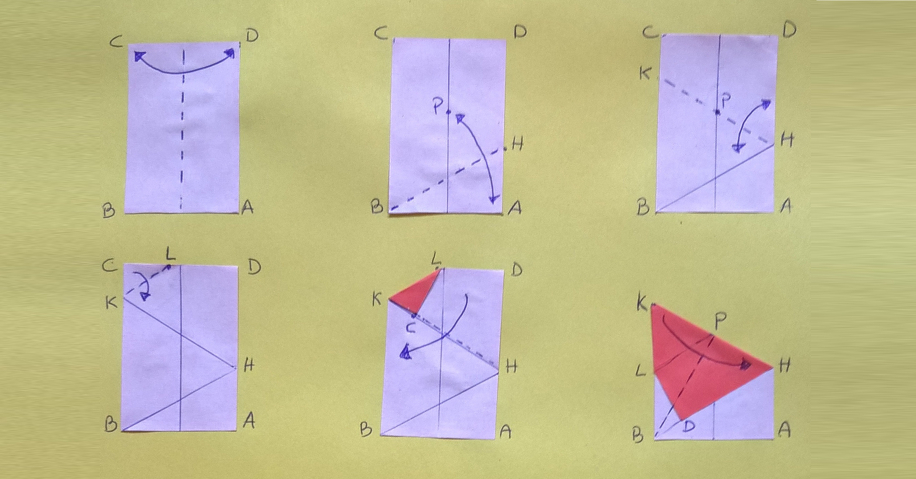
Di seguito le istruzioni di piegatura, per comprenderle meglio potete guardare i fotogrammi dei vari passaggi.
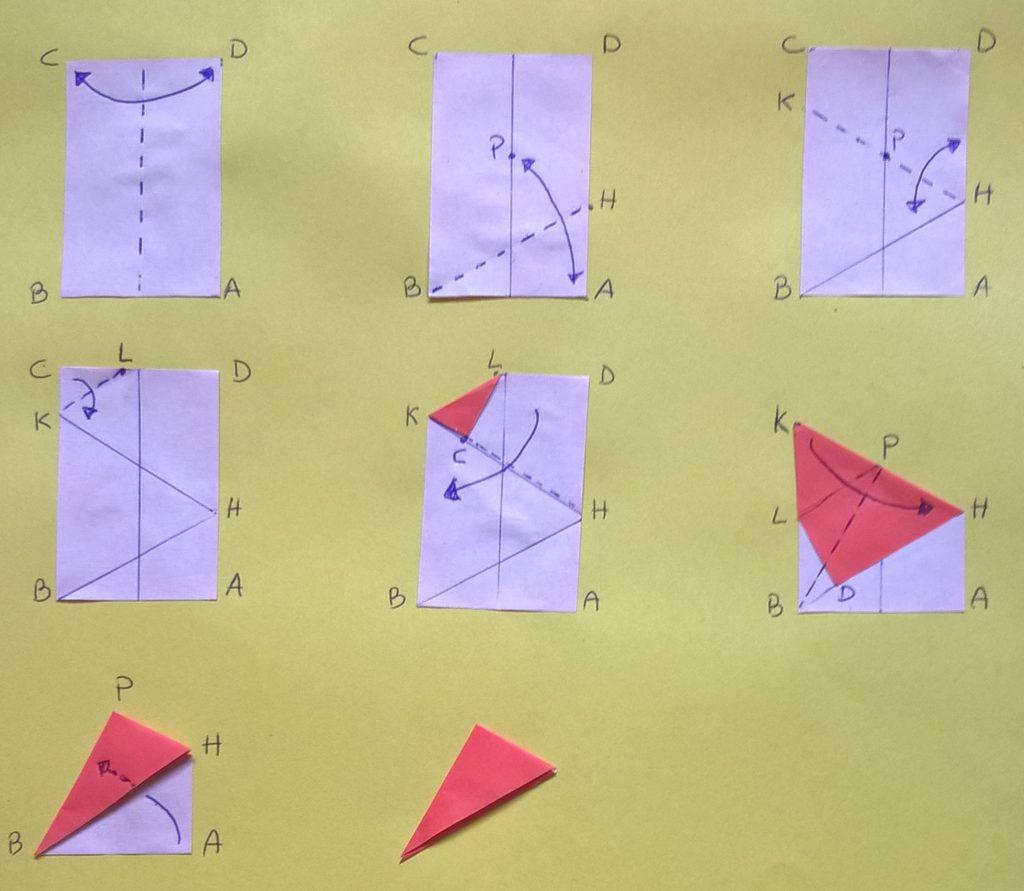
Ricordo che ogni immagine contiene l’istruzione della piega da eseguire il cui risultato compare nella figura successiva. In questo modello le pieghe da eseguire, indicate da linee tratteggiate, sono tutte a valle: una volta piegate e riaperte ricorderanno la valle scavata da un fiume. Le frecce a tratto continuo mostrano il movimento da eseguire; la freccia tratteggiata indica che la parte di carta piegata va intascata.
Ecco le istruzioni; l’obiettivo in ogni passaggio è quello di descrivere gli angoli che si formano. In alcuni casi completerò la domanda con la risposta per mostrare come usare le pieghe fatte, in altri casi suggerirò solo la domanda da porre ai ragazzi.
1. Portare il lato AD sul lato BC. La piega passa per i punti medi dei lati AB e CD ed è perpendicolare a essi: è dunque l’asse dei due segmenti e asse di simmetria del rettangolo.
2. Portare il vertice A sul punto P appartenente all’asse appena piegato in modo tale che la piega che si genera passi per il vertice B. Tale piega incontra il lato AD in H. Riaprire.
Quanto vale l’angolo ABH?
È abbastanza semplice notare che il triangolo ABP è equilatero. Infatti, è isoscele perché l’asse di simmetria del rettangolo ci garantisce che AP è congruente a BP; inoltre, BP è congruente ad AB perché i segmenti si sovrappongono nella piegatura. Da questo deduciamo che l’ampiezza dell’angolo ABP è 60° e quindi l’ampiezza dell’angolo ABH è 30°, essendo BH la bisettrice di ABP.
Osserviamo che l’ampiezza dell’angolo AHB è 60° e quindi l’ampiezza di BHD è 120° essendo il suo supplementare.
3. Portare il segmento HD su HB: D coinciderà con un punto interno ad HB e la piega incontrerà BC nel punto K. Riaprire.
Giustificare perché la piega fatta passa per P.
Qual è l’ampiezza degli angoli BHK e KHD?
La piega appena eseguita rappresenta la bisettrice dell’angolo BHD. Quindi entrambi gli angoli sono ampi 60°.
Calcolare l’angolo HKC (si può sfruttare il fatto che sia uno degli angoli del quadrilatero HKCD) e dedurre che il triangolo BHK è equilatero.
4. Portare il segmento KC sul segmento KH. La piega incontrerà CD in un punto L.
Descrivere il triangolo KCL.
La piega rappresenta la bisettrice di HKC e quindi l’ampiezza dell’angolo CKL è 60°; l’angolo in C è retto e, di conseguenza, l’angolo CLK è ampio 30°.
5. Senza riaprire la piega fatta al punto precedente, ripiegare lungo il segmento HK.
6. Piegare l’asse del segmento KH (portando K su H e sovrapponendo il segmento a se stesso) e riaprire.
Quanti triangoli di angoli di 30°-60°-90° si riescono a riconoscere?
Eccone alcuni: KBP, PBH, HBA (ed è facile dimostrare che sono tutti congruenti tra loro), BDL.
7. Ripiegare PB e successivamente piegare lungo BH intascando il vertice A.
Ecco pronta la squadretta 30°-60°-90°!
Un problema in più: nella costruzione occorre fare “sparire” il triangolo CKL (passaggio 4) . Se partissimo da un rettangolo di carta di lati AB e BK questo passaggio non sarebbe più necessario e la costruzione si completerebbe con meno carta. Chiedete ai vostri studenti di calcolare quanto dovrebbe essere lungo BK per produrre questi rettangoli di carta particolari.
