Il nostro orecchio distingue le note musicali in base alla loro frequenza, ossia al numero di oscillazioni al secondo dell’onda sonora.
Anche i colori non sono altro che diverse frequenze di un’onda elettromagnetica: quella che per noi è la luce visibile (anche se normalmente si usa la lunghezza d’onda in nanometri, più pratica rispetto alla frequenza).
Tuttavia le cellule del nostro occhio, a differenza di quelle dell’orecchio, non possono percepire la frequenza ma solo l’intensità luminosa. Come facciamo allora a vedere i colori?
Il trucco sta in una caratteristica di particolari cellule della retina chiamate “coni”: questi sono di tre tipi e ciascuno di essi è sensibile solo a una certa gamma di frequenze (colori), come se avesse davanti un filtro colorato.
Senza addentrarci nella fisiologia della percezione del colore e nelle teorie sviluppate già nel XIX secolo, ci basta sapere che questa caratteristica dell’occhio permette di simulare buona parte dei colori visibili combinando tre fonti luminose: una rossa, una verde e una blu.
Questo sistema è usato in tutti gli schermi a colori. Il nostro mBot, nella versione base, non ha uno schermo, ma ha due potenti LED tricromatici. Ciascuno di essi contiene in realtà tre LED distinti e indipendenti: per l’appunto uno rosso (R), uno verde (G) e uno blu (B).
Una premessa: per evitare possibili danni agli occhi, mai guardare direttamente questi LED da sopra quando sono accesi, se non da lontano.
Ci adeguiamo qui alla convenzione universale indicando i tre colori con le loro iniziali inglesi RGB (Red, Green, Blue). Attenzione quindi: G sta per “verde” e non per “giallo”.
Ora proviamo a generare i colori.
Costruiamo per lo sfondo di mBot il semplice script mostrato in Figura 2.
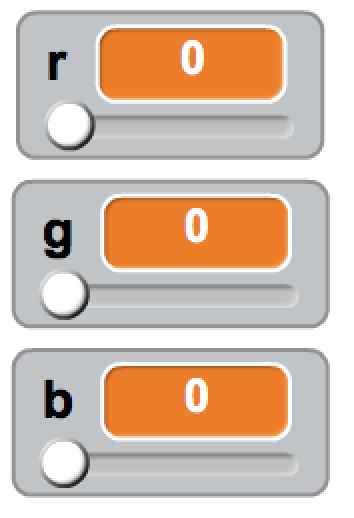
Nella sezione “Dati&Blocchi” andranno create le tre variabili “r”, “g” e “b”.
Impostiamo la visualizzazione delle variabili in modalità cursore (Figura 3), con un range di valori accettati che va da 0 a 100 per ciascuna variabile.
Avremmo quindi 101 x 101 x 101 = 1.030.301 combinazioni diverse.
Facciamo partire il programma e proviamo a muovere i cursori: ciascuno di essi controllerà la luminosità del LED corrispondente.
Se accendiamo più di un LED ne combiniamo le rispettive luci: ad esempio, illuminando sia il rosso (“r”) che il blu (“b”) il nostro occhio vedrà una luce viola… che in realtà non c’è: ci sono solo una luce rossa e una blu!
Per meglio vedere i colori può essere utile mettere un foglio di carta bianca, inclinato a 45 gradi, sopra mBot, come riflettore. E magari anche togliere l’eventuale copertura semitrasparente del robot (presente in alcune versioni de robot).
Notiamo che i LED accettano un valore fino a 255 (quindi in realtà avremmo a disposizione 256 x 256 x 256 = 16.777.216 diverse combinazioni), ma abbiamo volutamente lasciato 100 (il limite dei cursori, se non lo si cambia) per non produrre luci troppo intense.
Si può portare il limite a 255 se si vuole, ad esempio, proiettare il colore sul soffitto.
Facciamo un passo in più.
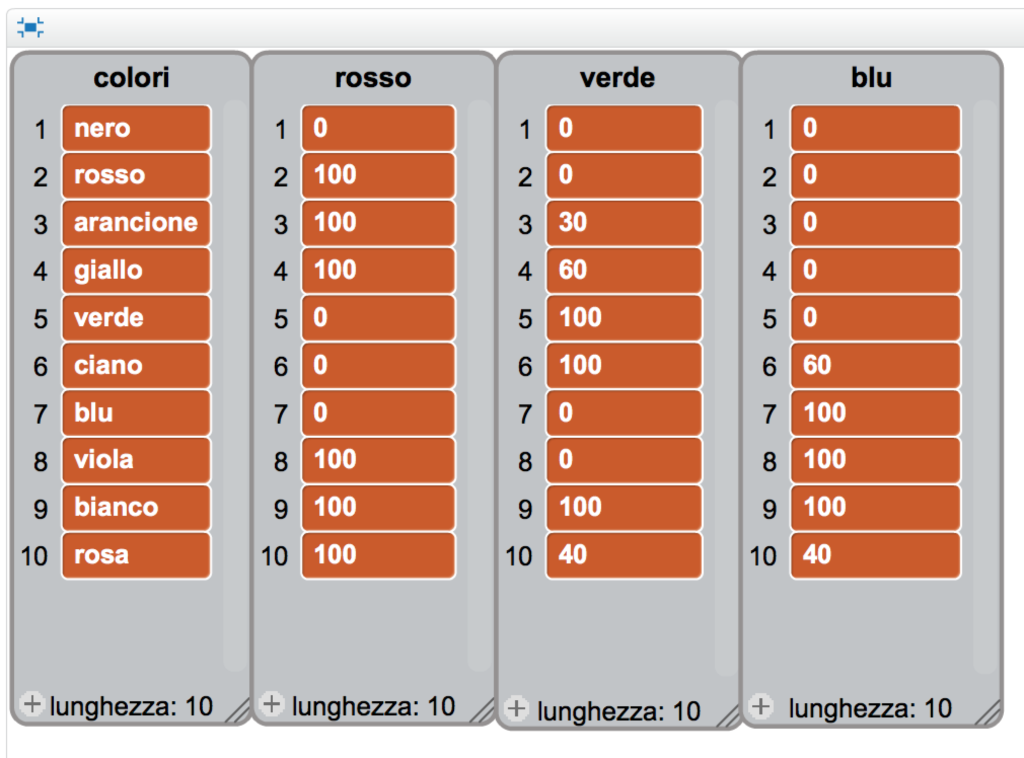
La Figura 4 (qui di lato) mostra un programma un pochino più complesso: abbiamo creato quattro liste (Figura 5) e le abbiamo disposte fianco a fianco.
La prima lista ha il nome di un colore e le altre tre indicano, sulla stessa riga, i valori RGB da mandare ai LED per ottenere quel colore.
Facendo partire il programma e scrivendo il numero della riga desiderata, ad esempio 3 per “arancione”, i LED produrranno quel colore… se abbiamo messo i numeri giusti nella riga corrispondente delle tre liste “rosso”, “verde” e “blu”.
Possiamo cambiare i numeri e riprovare anche senza fermare il programma. Possiamo anche togliere o aggiungere colori.
> Alcune note su questo programma:
I numeri mostrati non sono necessariamente i migliori: è importante sperimentare.
Notiamo che “arancione” e “giallo” sono due combinazioni di rosso e verde, differenti solo per la percentuale di verde: noi cambiamo una intensità e il nostro occhio percepisce un cambio di frequenza!
Il rosa è un esempio diverso dagli altri: non è altro che un rosso “annacquato” con l’aggiunta di un po’ di bianco. I colori tenui si possono ottenere in questo modo.
Le luminosità dei vari colori non sono tutte uguali. Sapreste uniformarle? (suggerimento: dividere ciascun colore per la somma r+g+b e poi riportare a 0…100 prima di usare imposta led…).
Non c’è controllo che la riga richiesta esista nella lista, ma se non c’è il valore di elemento… è 0, che in questo caso ci va bene perché otteniamo il nero.
Buon divertimento con la colorimetria!
Chi desiderasse approfondire la materia scoprirà che è interessante… e complessa.
MATERIALE ULTERIORE PER I DOCENTI CHE HANNO ADOTTATO
Volendo approfondire l’argomento colori con Scratch da un diverso punto di vista, è possibile studiare il funzionamento del programma con i file qui allegati. (Figura 1)
Si consiglia di eseguirlo in “Modalità turbo” (Figura 2).
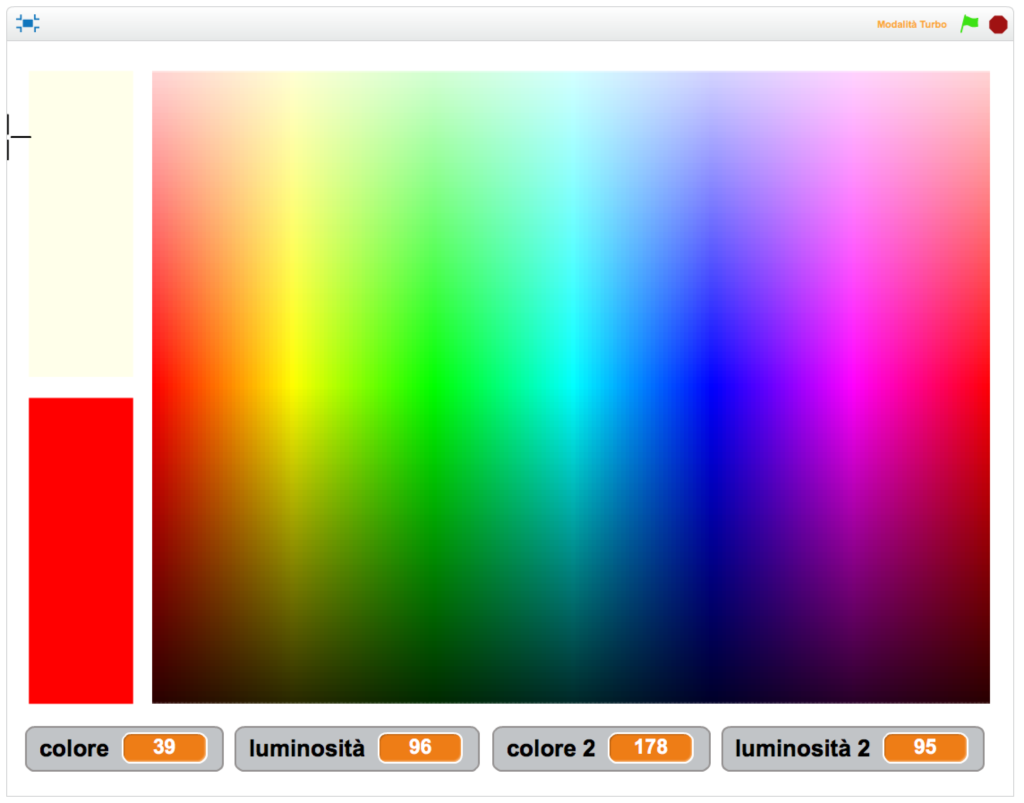
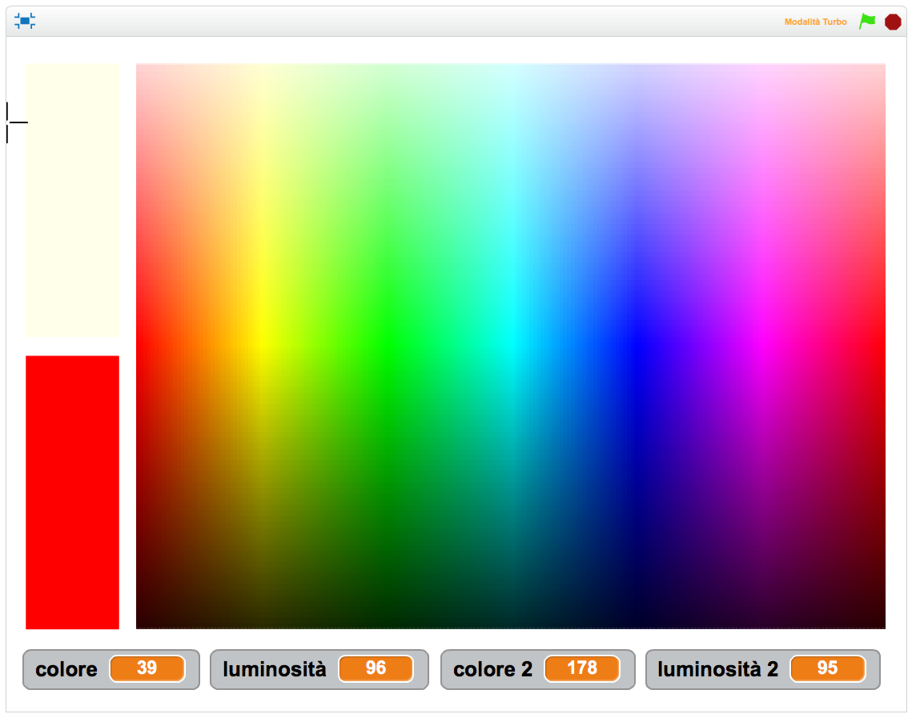
Dopo aver cliccato sulla bandierina verde, si muove il puntatore del mouse sulla palette colori e si clicca con il tasto sinistro per fissare il colore scelto sul riquadro in basso a sinistra.
Vediamo che questo programma utilizza il modello colori di Scratch, che prevede due parametri:
“colore”, il cui valore può andare da 0 a 199 (e dove 0 è rosso, 70 verde, 130 blu, 170 magenta e così via fino a tornare al rosso);
“luminosità”, il cui valore può andare da 0 (minimo) a 100 (massimo).
Notiamo anche che il valore di “colore” è disposto lungo l’asse orizzontale, mentre il valore di “luminosità” è disposto lungo l’asse verticale
di Enrico Colombini