
È noto che il linguaggio simbolico della Matematica ha continuamente bisogno, per essere efficacemente utilizzato, sia di poter essere collegato ai significati che lo hanno originato sia di poter essere tradotto e interpretato in linguaggi differenti, per esempio quello verbale o grafico o iconico. Se ciò non accade, il linguaggio simbolico diventa un ostacolo, diventa origine di difficoltà e fraintendimenti e spesso ciò favorisce, da parte degli alunni, un atteggiamento di imitazione meccanica e mnemonica di procedimenti stereotipati.
Come insegnanti sapete bene quanto sia essenziale la gestione consapevole dei vari linguaggi che la Matematica utilizza e anche la flessibilità nel passare da un tipo di linguaggio a un altro. Padroneggiare sia le diverse rappresentazioni dei numeri o delle forme del piano e dello spazio sia le rappresentazioni di dati in tabelle e grafici cartesiani costituisce un traguardo importante al termine della scuola secondaria di primo grado, come suggeriscono esplicitamente le Indicazioni Nazionali, e richiede che si dedichi tempo e spazio, in tutto il primo ciclo, alla lenta maturazione di questa competenza.
In questo e nei successivi contributi vi propongo dunque alcune attività orientate al tema delle rappresentazioni, con l’obiettivo di porre attenzione ad alcune di esse (tabelle, schemi a frecce, grafici cartesiani e grafi ad albero) sia nella fase della loro interpretazione che in quella della loro produzione.
La situazione che descrivo qui e di cui vi lascio anche la scheda da condividere con i vostri studenti potrebbe essere un’attività da proporre (in presenza ma anche a distanza) a inizio della scuola secondaria, da svolgere in modalità di collaborazione, a coppie o a gruppi più ampi e da affrontare senza ricorso a procedimenti noti, così da poter poi discutere, commentare e condividere le strategie e le osservazioni scaturite dai ragazzi. È ovvio, tuttavia, che potreste utilizzarla anche più avanti, come prova individuale, per saggiare la situazione cognitiva dei vostri alunni in merito alle richieste che il compito presenta.
Due scale per le temperature
La scala più usata per misurare le temperature è la scala Celsius, ma nei paesi anglosassoni è in uso anche la scala Fahrenheit.
Se indichi con la lettera $\text{C}$ la misura della temperatura espressa in gradi Celsius e con la lettera $\text{F}$ la misura espressa in gradi Fahrenheit, tra le due misure esiste la seguente relazione:
$\text{F}=\dfrac{9}{5}\text{C}+32$ *
1) La tabella contiene misure di temperatura espresse nel sistema Celsius. Completa la tabella:
| Celsius | $0$° | $5$° | $10$° | $15$° | $20$° | $25$° | $50$° | $75$° | $100$° |
| Fahrenheit |
2) La temperatura del corpo umano in condizioni normali è intorno ai $36,5$° Celsius. A quanti gradi Fahrenheit corrisponde?
3) Vogliamo ora trovare la relazione che permette di calcolare la misura in gradi Celsius quando si conosca quella in gradi Fahrenheit. Il procedimento che permette di calcolare $\text{F}$ a partire da $\text{C}$, secondo la relazione *, può essere rappresentata nel modo che segue:
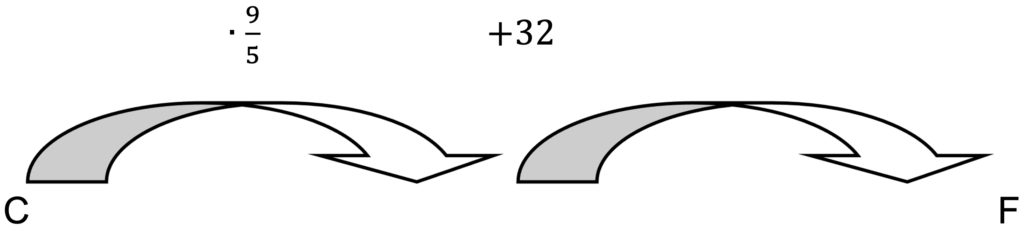
Invertendo il cammino, cioè partendo da $\text{F}$ e arrivando a esprimere $\text{C}$, come è necessario cambiare gli operatori $+32$ e $\cdot \frac{9}{5}$?
In conclusione, puoi dunque scrivere $\text{C}=$ ……………………..
È evidente che le prime due richieste sono molto semplici: il primo punto richiede la comprensione del testo proposto e il calcolo dei valori di $\text{F}$, a partire dai valori di $\text{C}$ assegnati in tabella, con l’utilizzo della formula assegnata *, così da ottenere la tabella che segue:
| Celsius | $0$° | $5$° | $10$° | $15$° | $20$° | $25$° | $50$° | $75$° | $100$° |
| Fahrenheit | $32$° | $41$° | $50$° | $59$° | $68$° | $77$° | $122$° | $167$° | $212$° |
Analogamente, se la temperatura del corpo umano in condizioni normali è intorno ai $36,5$° Celsius, sempre attraverso la stessa formula * si ottiene che questi corrispondono a $97,7$° gradi Fahrenheit.
La richiesta finale, al punto 3), ha l’obiettivo di illustrare, qualora non sia ancora familiare agli alunni, la rappresentazione del procedimento di calcolo proposto dalla formula * attraverso un grafo a frecce, un mediatore molto interessante per sostenere la formulazione di un procedimento inverso. Naturalmente questa parte può essere risolta anche con una semplice equazione, qualora gli alunni abbiano già questa competenza, tuttavia anche in questo caso potrebbe essere utile proporre loro questa efficace rappresentazione, che ha il pregio di mettere bene in evidenza il processo di inversione di una successione di operatori (nel nostro caso si tratta di due soli operatori ma si intuisce facilmente come il procedimento si possa generalizzare).
Gli operatori $+32$ e $\cdot \frac{9}{5}$ si invertono in $-32$ e $:\frac{9}{5}$ (equivalente a $\cdot \frac{5}{9}$ ) e dunque si ottiene $C=\left( F-32\right) \cdot \frac{5}{9}$.
Come insegnanti sapete bene che l’inversione di formule e in generale i procedimenti inversi costituiscono una difficoltà che riemerge spesso in varie occasioni e favorisce apprendimenti meccanici a scapito della comprensione di procedure anche semplici.
La rappresentazione degli operatori aritmetici ($+k$, $-k$, $\cdot k$, $:k$) con grafi a frecce offre la possibilità di visualizzare in un modo molto naturale (una freccia “che va” e l’altra “che torna”) un operatore e il suo inverso, noto, ovviamente, che $+k$ e $-k$ sono uno l’inverso dell’altro (e così pure $\cdot k$ e $:k$).
Con uno schema a frecce risulta molto semplice invertire una successione di due o più operatori aritmetici: rappresentato il “cammino di andata”, da sinistra a destra, si ottiene subito il “cammino di ritorno”, da destra a sinistra, invertendo le frecce insieme ai rispettivi operatori. In particolare, viene anche visualizzato correttamente l’ordine in cui tali operatori devono essere applicati.
La visualizzazione con frecce degli operatori aritmetici, che si colloca anche a un livello di efficace immagine mentale, può aiutare i ragazzi a cogliere l’aspetto funzionale nei problemi (per esempio a “vedere” la funzione $x\rightarrow kx$ in problemi di proporzionalità diretta) e questo a favore della costruzione del concetto generale di funzione e di funzione inversa.
Come ben sapete, l’algebra è uno strumento molto potente, che tuttavia spesso non è del tutto compreso: questo tipo di visualizzazione, collegata alla opportuna traduzione in espressione simbolica, può costituire un passaggio intermedio verso la generalità del linguaggio algebrico e favorirne una comprensione più profonda.
