
Come vi avevo anticipato nel precedente articolo, in questo vi voglio proporre alcune riflessioni sviluppate anni fa nell’ambito di esperienze svolte con alunni di $13$-$14$ anni nel contesto della probabilità e più specificatamente nell’utilizzo di grafi ad albero: mi sembrano riflessioni utili ancora oggi perché, partendo dall’analisi di alcuni errori, è possibile comprendere meglio come questo mediatore grafico possa risultare efficace non solo per arricchire le strategie di pensiero dei ragazzi ma anche per voi insegnanti, per cogliere maggiormente i processi di pensiero dei vostri alunni e supportarli di conseguenza.
Come già accennato nei miei articoli precedenti, l’importanza di promuovere negli studenti codici differenti da quello verbale poggia su quanto la ricerca ha messo in evidenza sulle connessioni tra rappresentazioni grafiche, immagini mentali e concetti della matematica. Tali risultati si possono, in sintesi, esprimere così:
- l’uso sistematico di adeguate rappresentazioni grafiche può influire positivamente sia sui processi di costruzione dei concetti che sulle strategie di soluzione dei problemi;
- è possibile intervenire intenzionalmente sulle capacità di visualizzazione di un individuo, cioè sulle sue capacità di costruire, scegliere, interpretare una rappresentazione grafica in relazione a un compito cognitivo assegnato.
È in quest’ottica quindi che vi presento il problema seguente, che potrete proporre ai vostri alunni quando abbiano già familiarizzato con i grafi ad albero in ambito probabilistico. Il mio consiglio, come al solito, è quello di proporre l’attività a piccoli gruppi, non importa se in presenza o a distanza; ciò che conta è che ci siano più idee da condividere poi in una discussione collettiva, durante la quale voi insegnanti potrete sviluppare un confronto critico e costruttivo da cui far emergere la formulazione di una sintesi.
Il cuoco distratto
In un ristorante la probabilità che il cuoco bruci l’arrosto è $0,02$, la probabilità che si dimentichi di salare l’acqua della pasta è $0,1$ e la probabilità che la sali troppo è ancora $0,1$. Qual è la probabilità che il pranzo preparato da quel cuoco riesca bene, supponendo che non faccia altri errori?
In questo caso gli eventi che interessano sono due, la buona riuscita dell’arrosto e la buona riuscita della cottura della pasta e si vuole che si verifichino entrambi. In base ai dati del testo, la situazione può essere rappresentata con un grafo ad albero in questo modo:
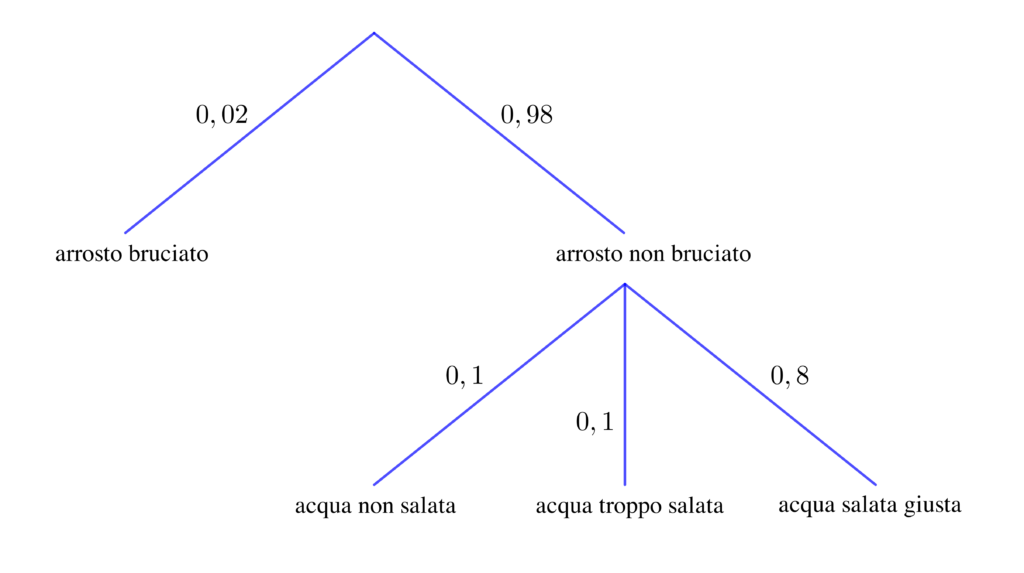
Dal grafo si ricava subito che c’è un solo cammino che ci interessa, quello composto dal ramo “arrosto non bruciato” e dal ramo “acqua salata giusta”, dunque
$p\left(\text{arrosto non bruciato e acqua salata giusta}\right)=p\left( \text{pranzo OK}\right)=0,98\cdot0,8=0,784$
Nelle ipotesi del testo, in conclusione, il pranzo di quel cuoco riesce bene nel $78,4\%$ dei casi.
Si può notare che il grafo non è stato completato, al secondo livello riguardante l’acqua per la pasta, nel caso dell’evento “arrosto bruciato”, perché questo non interessa certo ai fini della domanda proposta, relativa alla riuscita ottimale del pranzo. È da osservare inoltre che il grafo potrebbe essere costruito a partire dai tre rami riguardanti l’acqua per la pasta, collocando poi, dopo il ramo “acqua salata giusta”, i due rami riguardanti l’arrosto; in altre parole, i due livelli del grafo si possono scambiare e le probabilità scritte lungo i rami non cambiano perché si tratta di eventi indipendenti, cioè che non si influenzano a vicenda.
È anche possibile costruire un grafo più compatto, che gli alunni imparano ad apprezzare e che spesso propongono loro stessi, come il seguente:
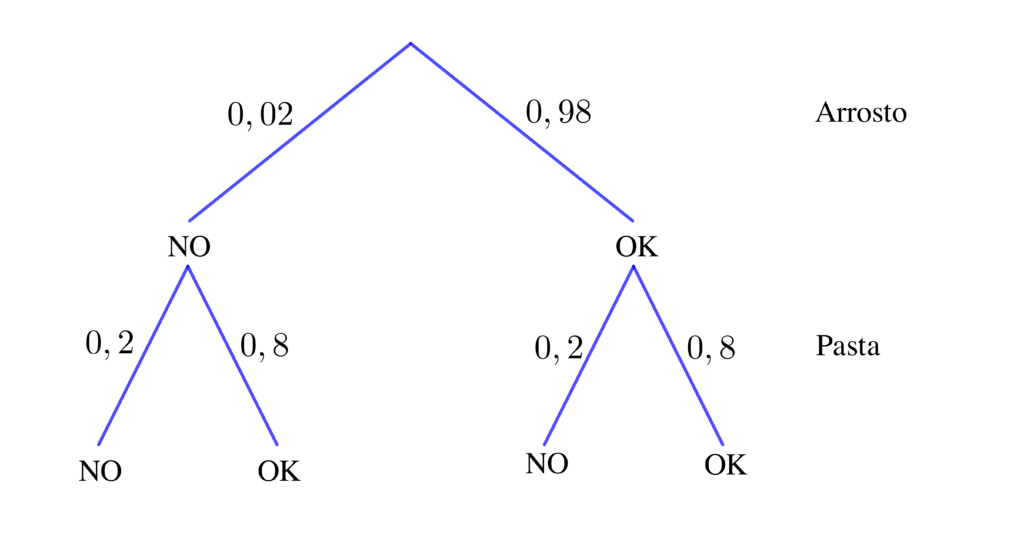
Il simbolismo accanto ai rami è facilmente interpretabile e relativamente alla pasta gli eventi sfortunati “acqua troppo salata” e “acqua non salata” sono compattati in un semplice “NO”, che comprende entrambi gli eventi. In termini più formali, si può dire che in questo caso l’evento “NO” è l’unione dei due eventi disgiunti “acqua troppo salata” e “acqua non salata”, per cui $p\left(\text{NO}\right)=0,1+0,1=0,2$.
E anche ora, con il simbolismo proposto, si ottiene lo stesso esito:
$p\left(\text{OK, OK}\right)=0,98\cdot0,8=0,784$
Tra gli errori che gli alunni potrebbero compiere nell’utilizzare un grafo ad albero per rappresentare la situazione descritta potrebbe esserci uno schema di questo tipo:
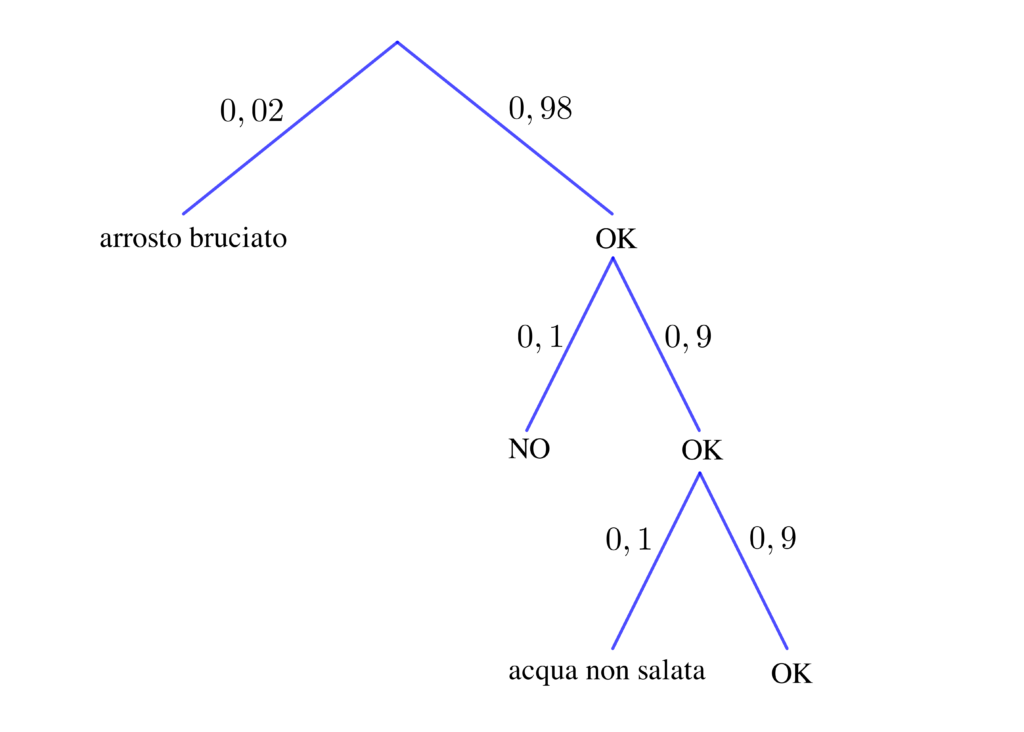
La soluzione, scorretta, che se ne potrebbe dedurre è che la probabilità che il pranzo riesca bene è data dal prodotto $0,98\cdot0,9\cdot0,9$. Il fraintendimento è dovuto al fatto che mentre i primi due rami, quelli relativi all’arrosto, sono corretti, è sbagliato invece rappresentare gli eventi relativi all’acqua per la pasta nel modo proposto, cioè su due livelli diversi: a ogni livello del grafo devono comparire tutte le possibili alternative e nel caso dell’acqua per la pasta il problema ci dice che queste sono esattamente tre: il cuoco sala troppo l’acqua, si dimentica di salarla oppure la sala nel modo giusto.
Vorrei osservare, inoltre, che la soluzione corretta può essere trovata anche senza l’ausilio di un grafo ad albero. Nelle esperienze in classe è capitato talvolta che alcuni alunni proponessero direttamente, come risposta corretta, il prodotto
$\left( 1-0,02\right) \left[ 1-\left( 0,1+0,1\right) \right] =0,98\cdot0,8=0,784$
È evidente che il primo fattore si riferisce all’evento “l’arrosto non è bruciato”, il secondo fattore si riferisce all’evento “l’acqua della pasta è salata giusta” ed entrambi gli eventi sono visti come complementari dei rispettivi eventi sfortunati. Poiché si tratta di eventi indipendenti fra loro la probabilità che il pranzo riesca bene è dato dal prodotto delle probabilità considerate. Questo tipo di soluzione richiede comunque una buona padronanza dei significati dei concetti in gioco.
Molto spesso, nelle soluzioni di chi non utilizza un grafo ad albero, si trova come risposta il seguente errore:
$p\left(\text{pranzo OK}\right)=1-\left(0,02+0,1+0,1\right)=1-0,22=0,78$
Non è facile, in questo caso, rendersi conto che la probabilità tra parentesi non è la probabilità dell’evento sfortunato, cioè che il cuoco bruci l’arrosto oppure che non sali l’acqua nel modo ottimale. Vediamo come occorre procedere: la probabilità dell’evento sfortunato va scritto per esteso così:
$p\left(\text{pranzo NO}\right)=p\left(\text{arrosto bruciato}\right)+p\left(\text{acqua salata troppo o non salata}\right)+$
$-\left(p\left(\text{arrosto bruciato e acqua salata troppo}\right)+p\left(\text{arrosto bruciato e acqua non salata}\right)\right)=$
$=0,02+\left(0,1+0,1\right)-\left(0,02\cdot0,1+0,02\cdot0,1\right)=0,02+0,2-0,004=0,216$
concludendo poi con
$p\left(\text{pranzo OK}\right)=1-0,216=0,784$
Per esplorare in modo alternativo la situazione ma anche per comprendere meglio l’errore descritto e capire quali siano gli eventi “unione” o “intersezione” in gioco, potrebbe essere utile una tabella a doppia entrata, come la seguente, dove è possibile leggere la risposta corretta nell’unica casella corrispondente al fatto che il pasto sia riuscito. Nella tabella sono ben evidenti gli altri eventi: il rettangolo a righe orizzontali relativo al caso “arrosto bruciato” e il quadrato a righe oblique relativo ai casi “acqua salata troppo” e “acqua non salata”. Sono ben visibili, qui, gli eventi intersezione di cui è necessario tenere conto e che invece non sono stati considerati nell’errore prima descritto, cioè “arrosto bruciato e acqua salata troppo” e “arrosto bruciato e acqua non salata”:
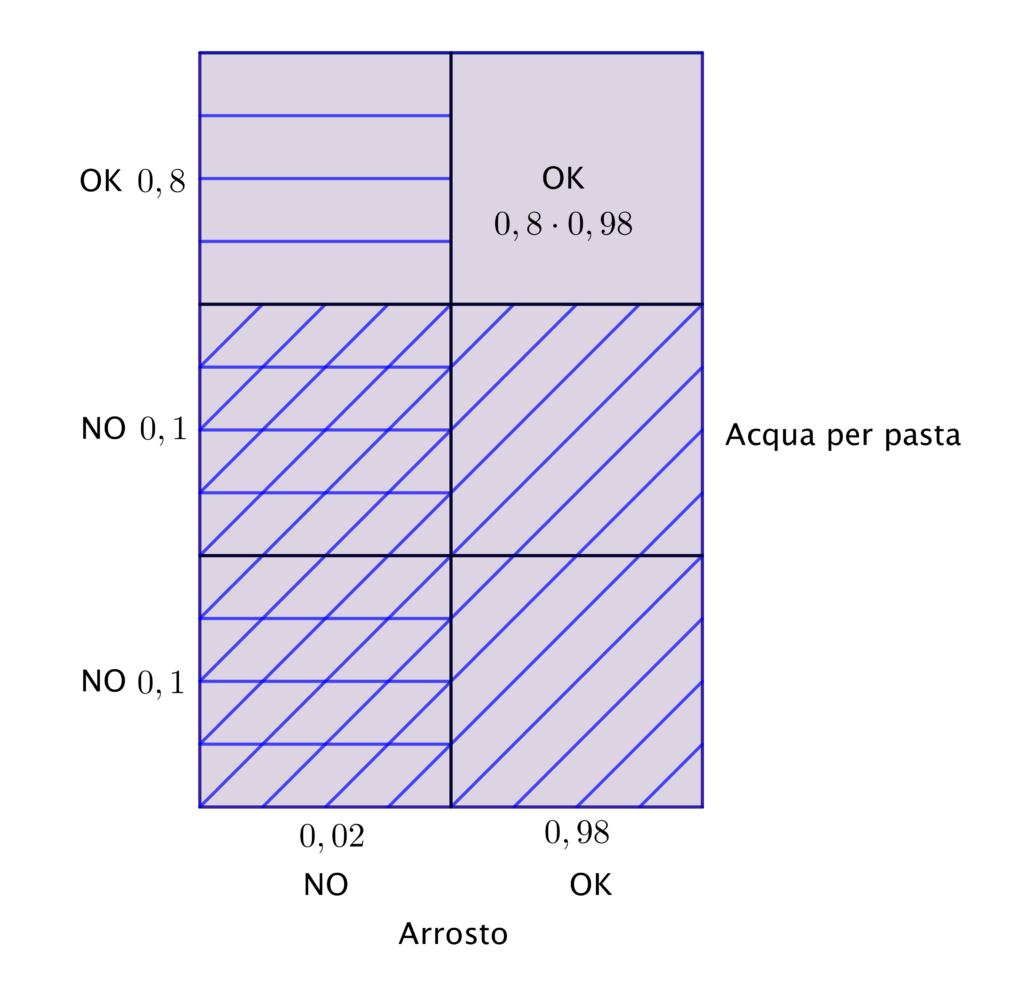
Nel caso del grafo ad albero abbiamo dunque visto che non è banale dominarne appieno le regole del gioco, che sono in sintesi le seguenti: a ogni livello del grafo i rami devono rappresentare eventi disgiunti e questi eventi devono esaurire tutti i casi possibili (a ogni livello abbiamo dunque una partizione degli eventi possibili). Rispettare queste regole risulta facile con eventi come per esempio le estrazioni successive da un’urna (con o senza reimbussolamento) ma nel caso del problema del cuoco distratto commentato qui abbiamo visto che la situazione è più complessa, perché il ricorso al grafo richiede maggiore consapevolezza. Riuscire tuttavia a costruirlo in modo corretto consente di dominare più facilmente la situazione problematica e aiuta a cogliere subito la strategia risolutiva corretta.
Mi auguro che quanto vi ho descritto possa essere motivante per promuovere con i vostri alunni confronti e dibattiti (a volte tutt’altro che banali) sulle rappresentazioni grafiche che vengono loro proposte o alle quali possono collegarsi spontaneamente nella soluzione di problemi o nella costruzione di concetti. Gli eventuali fraintendimenti, comunque, sono sempre buone occasioni di discussione e riflessione critica, sono momenti che arricchiscono il bagaglio culturale dei vostri alunni, dotandoli di più strumenti per approfondire e sviluppare le loro molteplici strategie mentali.
