
I capoluoghi di provincia offrono di solito servizi che sono più rari, o addirittura assenti, nei centri abitati più piccoli, come per esempio ospedali, grandi supermercati ecc. Purtroppo non è detto che gli abitanti di una provincia abbiano come città più vicina il corrispondente capoluogo.
Nella pianificazione di servizi regionali può essere utile domandarsi quali siano le aree più vicine a un capoluogo di provincia anziché a un altro: proviamo a farlo, nel caso semplice in cui non si tenga conto delle vie di comunicazione, degli ostacoli naturali ecc.
Il problema può essere risolto utilizzando un modello geometrico: il diagramma di Voronoi. Attraverso di esso si fissano dapprima particolari punti del piano – nel nostro caso i punti che rappresentano i capoluoghi di provincia – e si costruiscono in seguito le regioni piane costituite dai punti a essi più vicini.
Al termine di questa attività applicheremo il modello alla Lombardia, che presenta una situazione abbastanza complessa, vista la numerosità dei suoi capoluoghi.
Possiamo ragionare in modo semplice, considerando inizialmente due punti $A$ e $B$ nel piano cartesiano e ponendo alle studentesse e agli studenti alcuni quesiti, a cui dovrebbero saper rispondere per i loro studi precedenti.
- Qual è il luogo geometrico dei punti equidistanti da $A$ e $B$?
- Qual è la regione di piano i cui punti hanno distanza da $A$ minore della distanza da $B$ e viceversa?
- Scrivi l’espressione analitica del luogo geometrico dei punti per cui la distanza da $A$ è minore della distanza da $B$.
Chiediamo loro di disegnare questo luogo geometrico con GeoGebra come segue, ottenendo così il diagramma di Voronoi per due punti fissati.
- Disegna due punti $A$ e $B$ nel piano cartesiano, per esempio $A\left( -4,2\right)$ e $B\left( 5,-2\right)$.
- Traccia l’asse $a$ del segmento $AB$. Qual è la regione di piano i cui punti sono più vicini ad $A$ che a $B$?
- Digita nella Barra di inserimento la disequazione che hai ottenuto, sostituendo ai simboli le coordinate di $A$ e $B$, per evidenziare la regione di piano in questione.
- Ripeti le considerazioni precedenti per arrivare a disegnare la regione di piano i cui punti sono più vicini a $B$ che ad $A$ (figura 1): ottieni così il diagramma di Voronoi relativo ai due punti $A$ e $B$.
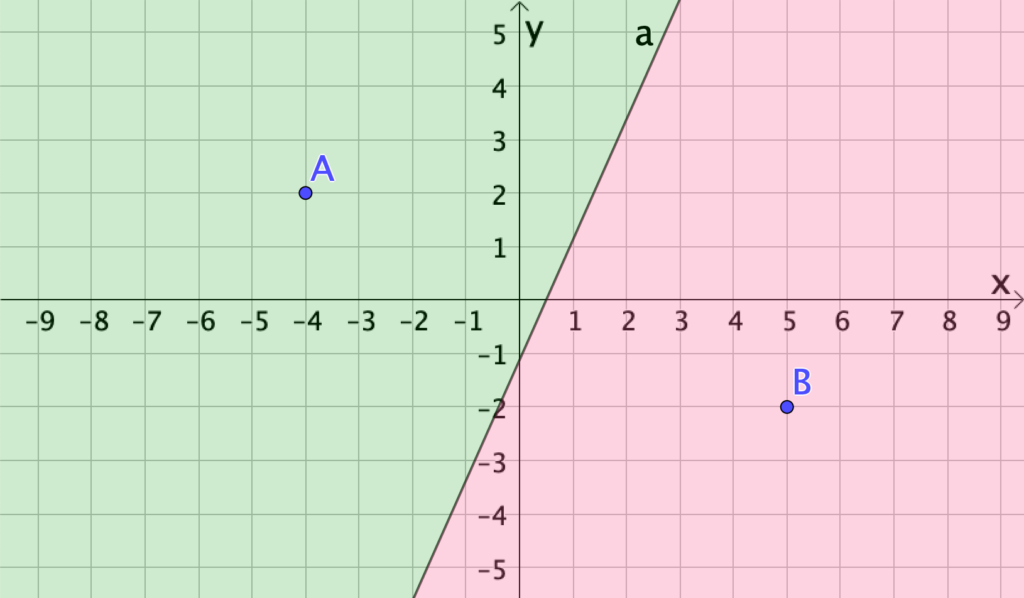
Approfondiamo l’analisi e aggiungiamo un punto rispetto alla situazione precedente. Invitiamo le studentesse e gli studenti a effettuare la seguente costruzione.
- Nascondi le regioni piane precedenti, lasciando visibile la retta $a$ e prendi un punto $C$, per esempio $C\left( -6,-5\right)$, e il triangolo $ABC$.
- Traccia gli assi dei lati $BC$ e $AC$ e indicali rispettivamente con $b$ e $c$; in seguito trova il loro punto di intersezione $H$. Che cosa rappresenta il punto $H$ per il triangolo $ABC$?
- Prendi un punto $E$ sulla retta $a$, al di sopra di $AB$, un punto $F$ sulla retta $b$, al di sotto di $BC$, un punto $G$ sulla retta $c$ a sinistra di $AC$ e disegna le semirette $HE$, $HF$, $HG$.
- Nascondi il triangolo $ABC$, le rette $a$, $b$, $c$, i punti $E$, $F$, $G$: le semirette che hai disegnato dividono il piano in tre regioni, che costituiscono il diagramma di Voronoi relativo ai punti $A$, $B$, $C$ (figura 2).
- Prendi un punto $P$ nel piano e traccia i segmenti $PA$, $PB$, $PC$. Muovilo nel piano e verifica che, quando si trova nella regione di Voronoi relativa a uno dei tre punti, la sua distanza da esso è minore delle distanze dagli altri due punti. Che cosa accade quando $P$ si trova sulle linee di confine?
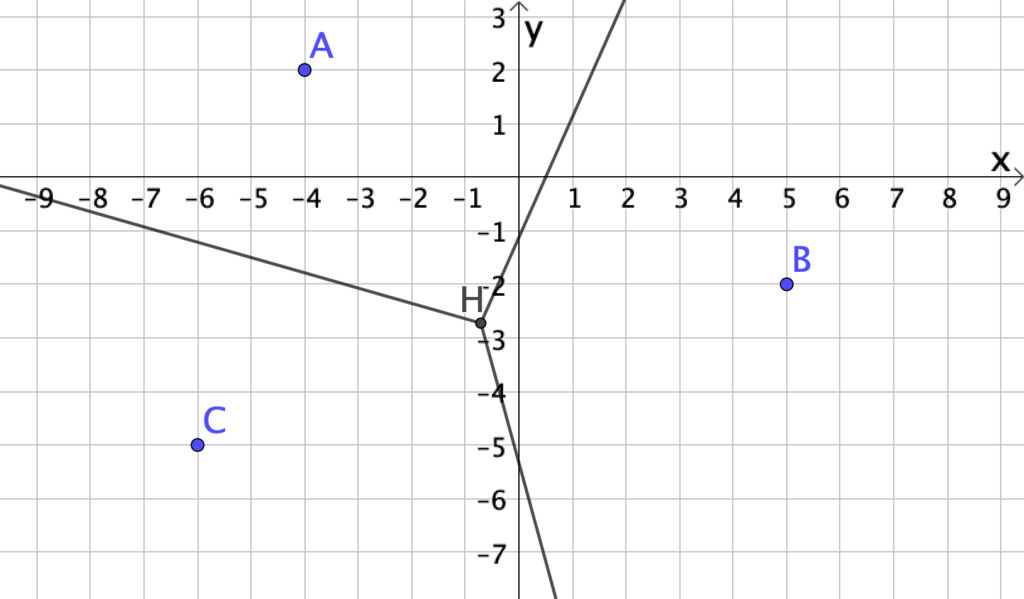
Analizziamo infine la situazione che si presenta con quattro punti.
- Nascondi $P$ e i tre segmenti $PA$, $PB$, $PC$, aggiungi un quarto punto $D$ alla costruzione, per esempio $D\left( 4,-9\right)$, e disegna il triangolo $BCD$.
- Traccia gli assi dei lati $CD$ e $BD$ e indicali rispettivamente con $p$ e $q$. Individua in seguito il loro punto di intersezione $K$.
- Prendi un punto $M$ su $p$, al di sotto di $K$, e traccia la semiretta $KM$; prendi un punto $N$ su $q$, a destra di $K$, e traccia la semiretta $KN$. Disegna il segmento $HK$ e nascondi la semiretta $HG$ della costruzione precedente. Il punto $K$ sta sulla semiretta $HF$. Perché?
- Nascondi il triangolo $BCD$, le rette $p$ e $q$, i punti $M$ e $N$: le semirette che hai disegnato e il segmento $HK$ dividono il piano in quattro regioni, che costituiscono il diagramma di Voronoi relativo ai punti $A$, $B$, $C$, $D$ (figura 3).
- Visualizza il punto $P$ nel piano e traccia il segmento $PD$; muovi $P$ nel piano e verifica che, quando $P$ si trova nella regione di Voronoi relativa a un certo punto, la sua distanza da quel punto è minore delle altre tre.
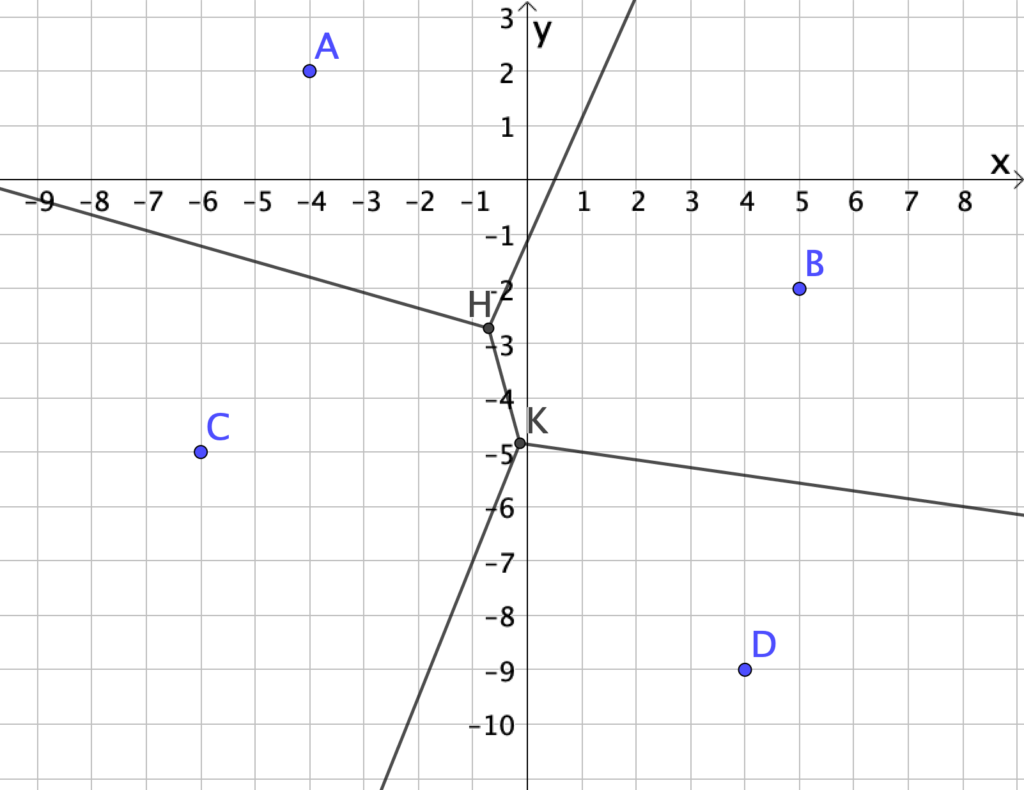
Ora che la procedura è compresa, le studentesse e gli studenti possono utilizzare in modo consapevole il comando di GeoGebra Voronoi (); tra le parentesi tonde è sufficiente inserire i punti. Utilizziamo questo comando per realizzare il diagramma di Voronoi che ha come punti fissi i capoluoghi di provincia della Lombardia.
- Apri il file già predisposto, in cui è stata importata la mappa delle province della Lombardia.
- Segna i punti corrispondenti alle città capoluogo di provincia.
- Utilizza il comando Voronoi per disegnare il diagramma.
- Come vedi, si tratta di un grafico che fuoriesce dai confini della regione di piano che rappresenta la Lombardia. Per disegnare il diagramma di Voronoi di una regione di piano finita occorre intersecare il grafico ottenuto tramite GeoGebra con i confini della regione considerata (figura 4).
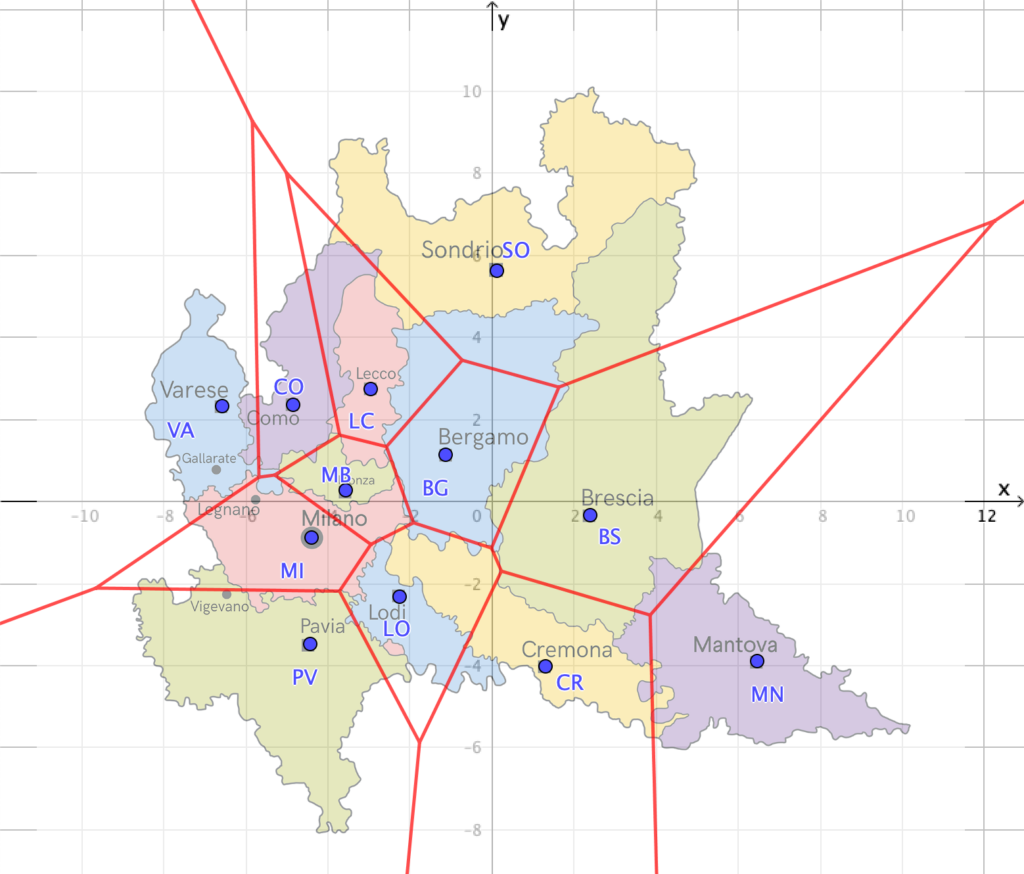
Questa attività di esplorazione è tratta da “Matematica allo specchio edizione Blu – II biennio e V anno”, il nuovo corso di Matematica edito da Ghisetti e Corvi.
