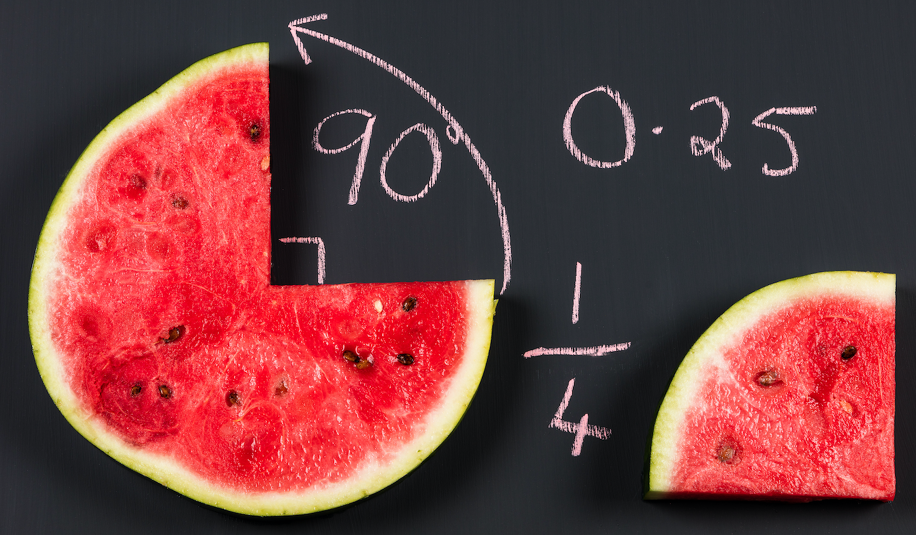
Se leggiamo sull’etichetta di una piccola bottiglia di acqua minerale che il contenuto è di $0,5$ l, associamo automaticamente questa misura a una frazione dell’intero, cioè a $\dfrac{1}{2}$ l. Allo stesso modo, se vogliamo adattare a una singola dose una ricetta di cucina che prevede, per $4$ persone, $1$ hg di zucchero, consideriamo che $\dfrac{1}{4}$ di $1$ hg corrisponde a $0,25$ hg, cioè a $25$ g di zucchero.
La trasformazione di semplici frazioni in decimali e viceversa è entrata nella nostra pratica quotidiana e ha a che fare con le misure, con le approssimazioni, con i calcoli; stupisce pensare che tale pratica sia relativamente giovane e sia nata soltanto sei secoli fa.

È infatti alla fine del $1500$ che Simon Stevin, ingegnere, fisico e matematico fiammingo, pubblica un volumetto intitolato La disme, in cui invita a trasformare le frazioni in decimali per poter applicare sui nuovi numeri con la virgola le stesse tecniche operative che già si usavano sui numeri interi.
Stevin scrive in un periodo storico in cui la conoscenza e l’abilità di “fare calcoli” non può più essere un lusso di pochi: alla fine del ‘$500$ l’incremento demografico determina una crescita della produzione industriale e dei commerci e la nascita delle prime banche. Saper “fare calcoli” consente di essere in grado di tutelare i propri diritti e i propri interessi e di non sottostare a sudditanza economica di chi “sa”.
Ho trovato interessante questo cenno storico alla nascita dei numeri decimali; confesso che non pensavo fossero numeri così giovani. Tuttavia, nella mia pratica didattica ho sempre dato molta importanza alle diverse rappresentazioni di un numero razionale e alle trasformazioni che conducono dall’una all’altra forma, sia essa frazionaria, decimale o percentuale.
Voglio soffermarmi qui sul passaggio da frazione a numero decimale; assodato che una frazione indica una divisione fra numeri interi, quali tipi di numeri decimali si ottengono dalla divisione tra numeratore e denominatore di una frazione?
Proponiamo alle nostre studentesse e ai nostri studenti un’attività di esplorazione che evidenzi i nodi concettuali della trasformazione di una frazione in numero decimale; l’attività può partire da una lezione dialogata, in cui l’insegnante gestisce la parte di lavoro che riguarda il software, oppure essere interamente affidata al lavoro in piccoli gruppi. Poniamo il problema: quale numero decimale si può associare alla frazione $\dfrac{41}{7}$?

Se eseguiamo l’operazione $41:7$ con una calcolatrice otteniamo un numero decimale finito, con una quantità di cifre decimali che varia da una calcolatrice all’altra. È questo il numero da associare alla frazione? O le cifre decimali di $\dfrac{41}{7}$ vanno oltre le cifre rappresentate dalla calcolatrice?
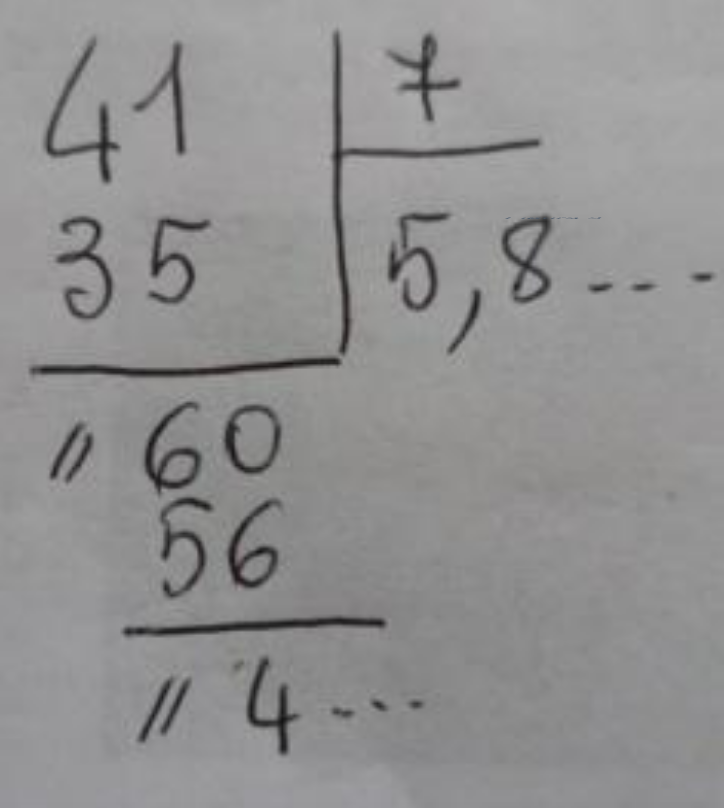
Proviamo a eseguire la divisione a mano, con il consueto algoritmo. Nell’affrontare il calcolo a mano ci rendiamo conto che il procedimento di divisione può andare avanti ancora e ancora… fino a quando? E da quali numeri è composto il quoziente?
Per evitare un calcolo ripetitivo chiediamo alle studentesse e agli studenti di elencare i passi dell’algoritmo della divisione a mano; implementiamo tali passi su un foglio di calcolo di GeoGebra attraverso una serie di istruzioni che li rappresentino. In sostanza:
- per trovare il quoziente intero tra dividendo e divisore usiamo il comando di GeoGebra Quoziente [dividendo, divisore];
- per trovare il resto parziale usiamo Resto [dividendo, divisore];
- moltiplichiamo per $10$ il resto parziale e ripetiamo i due passaggi precedenti.
Scriviamo nel foglio di calcolo le istruzioni indicate in figura, avendo cura di inserire a parte (nelle celle G$4$ e G$5$) i valori iniziali di dividendo e divisore.

Se copiamo e incolliamo le istruzioni della riga $3$ per un certo numero di righe (per esempio $20$), possiamo vedere la regolarità con cui vengono calcolati i resti e quindi i quozienti della divisione e fare alcune osservazioni in proposito.
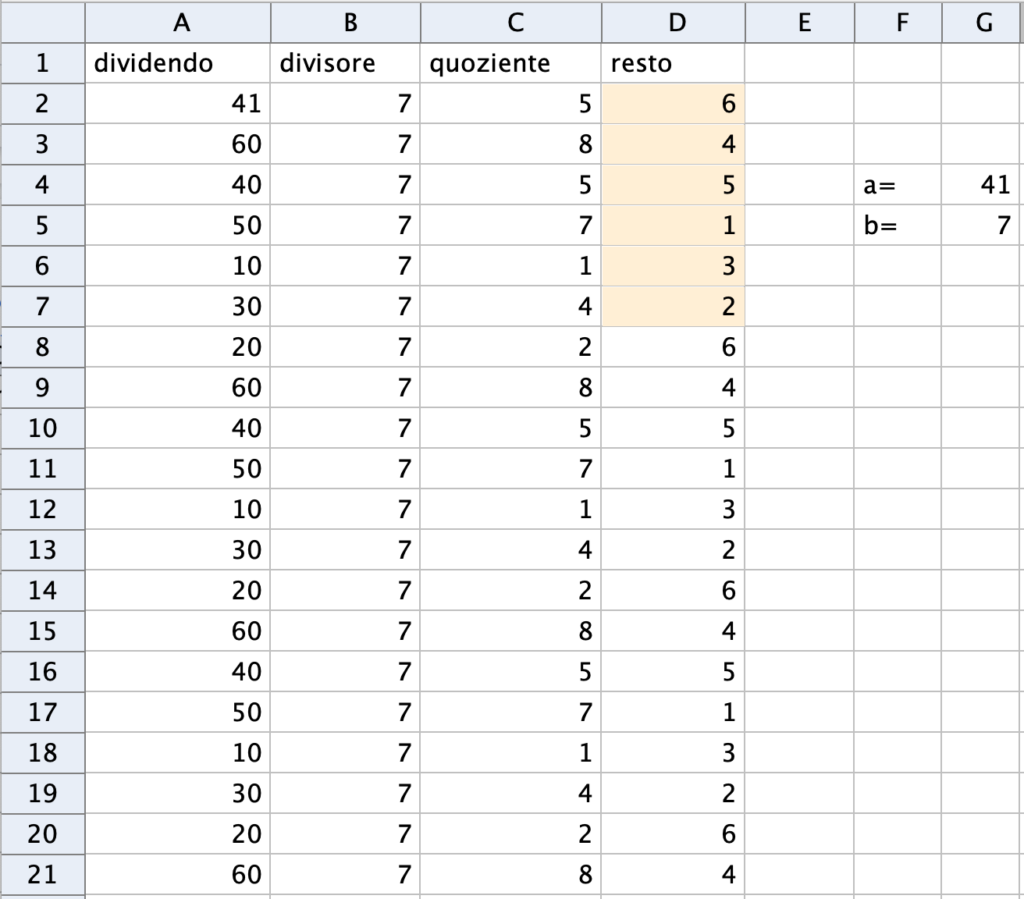
Poniamo alcune domande alle studentesse e agli studenti.
- Costruisci l’insieme dei resti parziali della divisione nell’ordine in cui sono stati ricavati. Quanti elementi ha?
- Tra essi c’è lo $0$? Potrebbe comparire nei passaggi successivi che non sono visualizzati sul foglio di calcolo? Perché?
Visualizziamo su un piano cartesiano la successione dei resti. Per evitare che i punti vengano etichettati selezioniamo dal menu Opzioni/Etichettatura il comando Nessun nuovo oggetto.
Numeriamo i resti: nella colonna I, a partire dalla cella I$2$ indichiamo i numeri naturali da $1$ a $20$.
Nella colonna J, a partire da J$2$, costruiamo le coordinate dei punti che hanno per ascissa il numero progressivo e per ordinata il resto corrispondente.

Copiamo e incolliamo le istruzioni indicate sino alla riga che contiene l’ultimo resto che abbiamo ricavato; GeoGebra disegna nel piano un insieme di punti, disposti con regolarità. Se vogliamo che questi punti vengano collegati in una spezzata creiamo la lista della colonna che contiene le coordinate e applichiamo a essa l’istruzione Spezzata(lista).
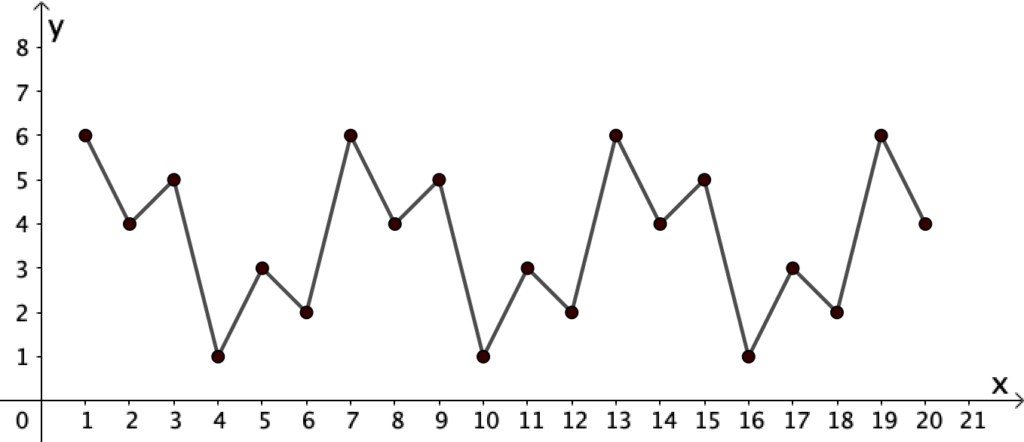
Chiediamo alle studentesse e agli studenti di descrivere il grafico:
- fra quali valori delle ordinate sono compresi i punti?
- il grafico ha un andamento periodico; che cosa significa, secondo te?
Adoperiamo ora il programma che abbiamo costruito per trovare quozienti e resti in altre divisioni. Facciamo doppio clic sulle celle G$4$ e G$5$ e modifichiamo i valori di $a$ e di $b$, procedendo come segue:
- prima cambiamo solo il dividendo $a$;
- in seguito cambiamo solo il divisore $b$, osservando che non può essere uguale a $0$;
- infine cambiamo sia il dividendo sia il divisore.
Chiediamo alle nostre studentesse e ai nostri studenti:
- indica quali tipi di numeri decimali si ottengono se
- il divisore contiene soltanto fattori $2$ e $5$;
- il divisore non contiene i fattori $2$ e $5$ oppure li contiene insieme ad altri.
- può accadere che il risultato sia un decimale infinito non periodico? Perché?
- come si può stabilire, osservando dividendo e divisore, se la divisione ha un risultato decimale finito o decimale illimitato?
Terminiamo l’attività sintetizzando i risultati ottenuti e formalizzando la teoria alla base della rappresentazione di una frazione in decimale.
Ricaviamo un feedback del lavoro svolto proponendo una gara: dopo aver diviso la classe in due gruppi chiediamo di riconoscere frazioni che danno origine a decimali finiti o periodici; ancora, chiediamo di valutare, dato un numero decimale periodico, il tipo di denominatore della frazione corrispondente ridotta ai minimi termini.
Questa attività di esplorazione è tratta da “Matematica allo specchio”, il nuovo corso di Matematica per la scuola secondaria di secondo grado edito da Ghisetti e Corvi.
